| << Chapter < Page | Chapter >> Page > |
Eliminate the parameter from the given pair of parametric equations and write as a Cartesian equation: and
When we are given a set of parametric equations and need to find an equivalent Cartesian equation, we are essentially “eliminating the parameter.” However, there are various methods we can use to rewrite a set of parametric equations as a Cartesian equation. The simplest method is to set one equation equal to the parameter, such as In this case, can be any expression. For example, consider the following pair of equations.
Rewriting this set of parametric equations is a matter of substituting for Thus, the Cartesian equation is
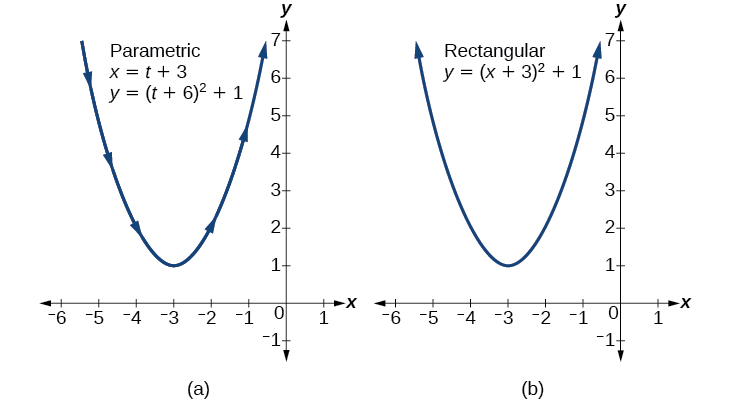
Use two different methods to find the Cartesian equation equivalent to the given set of parametric equations.
Method 1 . First, let’s solve the equation for Then we can substitute the result into the equation.
Now substitute the expression for into the equation.
Method 2 . Solve the equation for and substitute this expression in the equation.
Make the substitution and then solve for
Write the given parametric equations as a Cartesian equation: and
Although we have just shown that there is only one way to interpret a set of parametric equations as a rectangular equation, there are multiple ways to interpret a rectangular equation as a set of parametric equations. Any strategy we may use to find the parametric equations is valid if it produces equivalency. In other words, if we choose an expression to represent and then substitute it into the equation, and it produces the same graph over the same domain as the rectangular equation, then the set of parametric equations is valid. If the domain becomes restricted in the set of parametric equations, and the function does not allow the same values for as the domain of the rectangular equation, then the graphs will be different.
Find a set of equivalent parametric equations for
An obvious choice would be to let Then But let’s try something more interesting. What if we let Then we have
The set of parametric equations is
See [link] .
Access these online resources for additional instruction and practice with parametric equations.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?