| << Chapter < Page | Chapter >> Page > |
In many cases, we may have a pair of parametric equations but find that it is simpler to draw a curve if the equation involves only two variables, such as and Eliminating the parameter is a method that may make graphing some curves easier. However, if we are concerned with the mapping of the equation according to time, then it will be necessary to indicate the orientation of the curve as well. There are various methods for eliminating the parameter from a set of parametric equations; not every method works for every type of equation. Here we will review the methods for the most common types of equations.
For polynomial, exponential, or logarithmic equations expressed as two parametric equations, we choose the equation that is most easily manipulated and solve for We substitute the resulting expression for into the second equation. This gives one equation in and
Given and eliminate the parameter, and write the parametric equations as a Cartesian equation.
We will begin with the equation for because the linear equation is easier to solve for
Next, substitute for in
The Cartesian form is
Given the equations below, eliminate the parameter and write as a rectangular equation for
as a function
of
Eliminate the parameter and write as a Cartesian equation: and
Isolate
Substitute the expression into
The Cartesian form is
Eliminate the parameter and write as a Cartesian equation: and
Solve the first equation for
Then, substitute the expression for into the equation.
The Cartesian form is
Eliminate the parameter and write as a rectangular equation .
Eliminating the parameter from trigonometric equations is a straightforward substitution. We can use a few of the familiar trigonometric identities and the Pythagorean Theorem.
First, we use the identities:
Solving for and we have
Then, use the Pythagorean Theorem:
Substituting gives
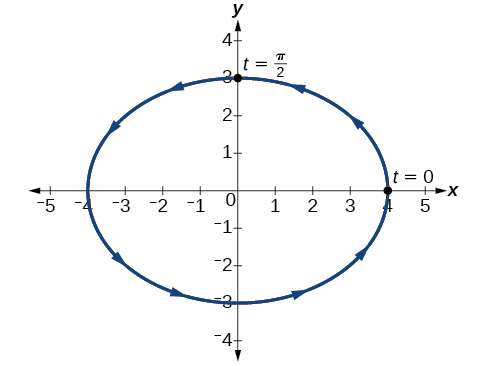
Eliminate the parameter from the given pair of trigonometric equations where and sketch the graph.
Solving for and we have
Next, use the Pythagorean identity and make the substitutions.
The graph for the equation is shown in [link] .

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?