| << Chapter < Page | Chapter >> Page > |
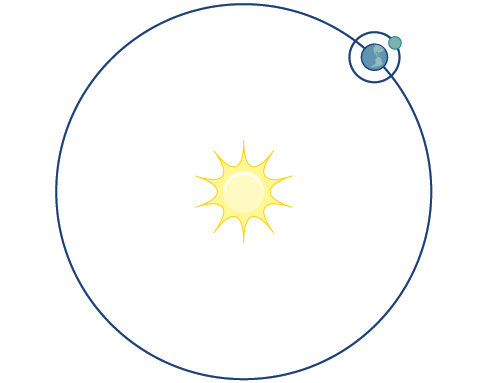
Consider the path a moon follows as it orbits a planet, which simultaneously rotates around the sun, as seen in [link] . At any moment, the moon is located at a particular spot relative to the planet. But how do we write and solve the equation for the position of the moon when the distance from the planet, the speed of the moon’s orbit around the planet, and the speed of rotation around the sun are all unknowns? We can solve only for one variable at a time.
In this section, we will consider sets of equations given by and where is the independent variable of time. We can use these parametric equations in a number of applications when we are looking for not only a particular position but also the direction of the movement. As we trace out successive values of the orientation of the curve becomes clear. This is one of the primary advantages of using parametric equations : we are able to trace the movement of an object along a path according to time. We begin this section with a look at the basic components of parametric equations and what it means to parameterize a curve. Then we will learn how to eliminate the parameter, translate the equations of a curve defined parametrically into rectangular equations, and find the parametric equations for curves defined by rectangular equations.
When an object moves along a curve—or curvilinear path —in a given direction and in a given amount of time, the position of the object in the plane is given by the x- coordinate and the y- coordinate. However, both and vary over time and so are functions of time. For this reason, we add another variable, the parameter , upon which both and are dependent functions. In the example in the section opener, the parameter is time, The position of the moon at time, is represented as the function and the position of the moon at time, is represented as the function Together, and are called parametric equations, and generate an ordered pair Parametric equations primarily describe motion and direction.
When we parameterize a curve, we are translating a single equation in two variables, such as and into an equivalent pair of equations in three variables, and One of the reasons we parameterize a curve is because the parametric equations yield more information: specifically, the direction of the object’s motion over time.
When we graph parametric equations, we can observe the individual behaviors of and of There are a number of shapes that cannot be represented in the form meaning that they are not functions. For example, consider the graph of a circle, given as Solving for gives or two equations: and If we graph and together, the graph will not pass the vertical line test, as shown in [link] . Thus, the equation for the graph of a circle is not a function.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?