0.7 Generalizations of the basic multiresolution wavelet system  (Page 3/28)

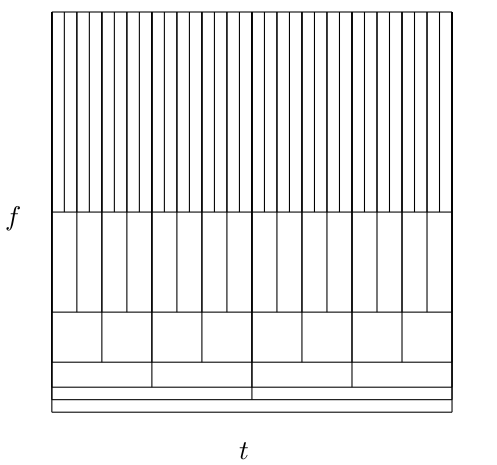
The tiling of the time-frequency plane is a powerful graphical method for understanding the properties of the DWT and for analyzing signals. Forexample, if the signal being analyzed were a single wavelet itself, of the form

the DWT would have only one nonzero coefficient, $d_2\left(2\right)$ . To see that the DWT is not time (or shift) invariant, imagine shifting $f\left(t\right)$ some noninteger amount and you see the DWT changes considerably. If the shiftis some integer, the energy stays the same in each scale, but it “spreads out" along more values of $k$ and spreads differently in each scale. If the shift is not an integer, the energy spreads in both $j$ and $k$ . There is no such thing as a “scale limited" signal corresponding to aband-limited (Fourier) signal if arbitrary shifting is allowed. For integer shifts, there is a corresponding concept [link] .

General tiling

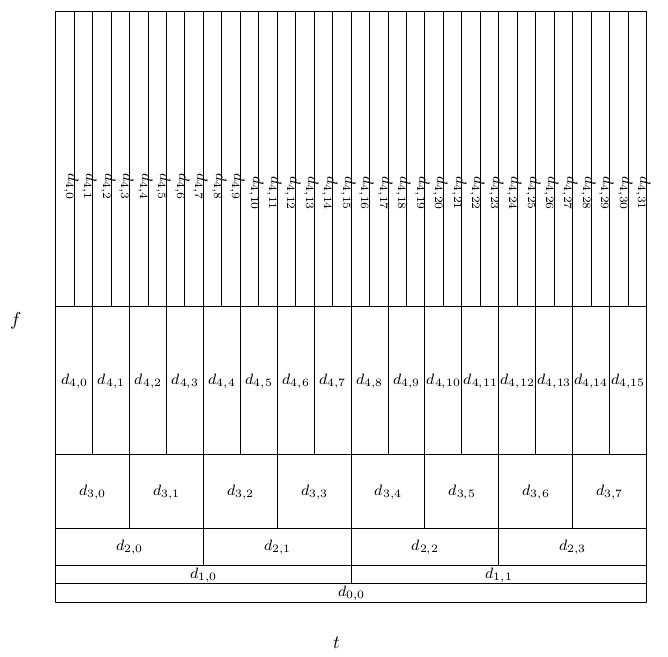
Notice that for general, nonstationary signal analysis, one desires methods for controlling the tiling of the time-frequency plane, not justusing the two special cases above (their importance notwithstanding). An alternative way to obtain orthonormal wavelets $\psi \left(t\right)$ is using unitary FIR filter bank (FB) theory. That will be done with M-band DWTs, waveletpackets, and time-varying wavelet transforms addressed in Section: Multiplicity-M (M-Band) Scaling Functions and Wavelets and Section: Wavelet Packets and   Chapter: Filter Banks and Transmultiplexers respectively.

Remember that the tiles represent the relative size of the translations and scale change. They do not literally mean the partitioned energy isconfined to the tiles. Representations with similar tilings can have very different characteristics.

Multiplicity-m (m-band) scaling functions and wavelets

While the use of a scale multiplier $M$ of two in [link] or [link] fits many problems, coincides with the concept of an octave, gives abinary tree for the Mallat fast algorithm, and gives the constant-Q or logarithmic frequency bandwidths,the conditions given in  Chapter: The Scaling Function and Scaling Coefficients, Wavelet and Wavelet Coefficients and Section: Further Properties of the Scaling Function and Wavelet can be stated and proved in a more general setting where the basic scaling equation [link] , [link] , [link] , [link] , [link] , [link] , [link] rather than the specific doubling value of $M=2$ . Part of the motivation for a larger $M$ comes from a desire to have a more flexible tiling of the time-scale plane than that resulting from the $M=2$ wavelet or the short-time Fourier transform discussed in Section: Tiling the Time–Frequency or Time–Scale Plane . It also comes from a desire for some regions of uniform band widths ratherthan the logarithmic spacing of the frequency responses illustrated in Figure: Frequency Bands for the Analysis Tree . The motivation for larger $M$ also comes from filter bank theory which is discussed in  Chapter: Filter Banks and Transmultiplexers .

We pose the more general multiresolution formulation where [link] becomes

In some cases, $M$ may be allowed to be a rational number; however, in most cases it must be an integer, and in [link] it is required to be 2. In the frequency domain, this relationship becomes