0.7 Generalizations of the basic multiresolution wavelet system  (Page 2/28)

Tiling with the discrete-time short-time fourier transform

The DSTFT basis functions are of the form

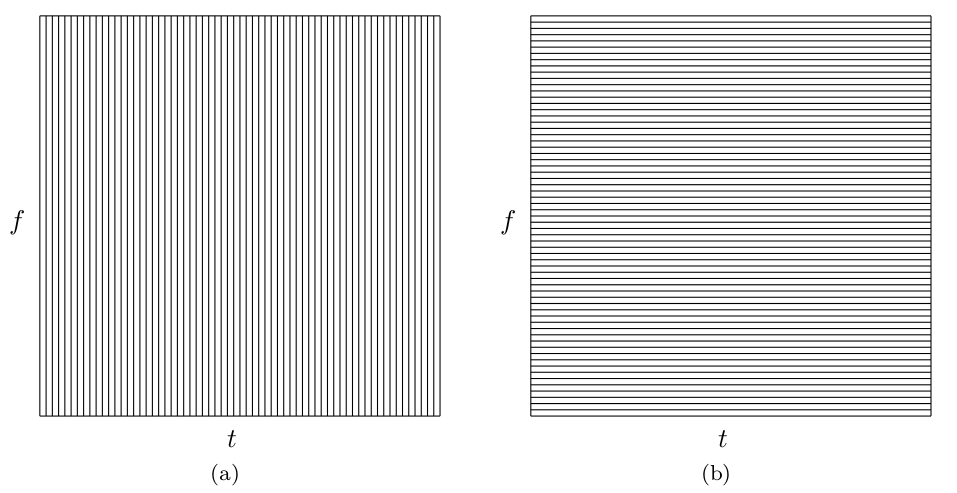
where $w\left(t\right)$ is a window function [link] . If these functions form an orthogonal (orthonormal) basis, $x\left(t\right)={\sum }_{j,k}〈x,,,w_{j,k}〉w_{j,k}\left(t\right)$ . The DSTFT coefficients, $〈x,,,w_{j,k}〉$ , estimate the presence of signal components centered at $(k{\tau }_0,j{\text{ω}}_0)$ in the time-frequency plane, i.e., the DSTFT gives a uniform tiling of the time-frequency plane with the basis functions $\left\{w_{j,k},\left(t\right)\right\}$ . If ${\text{Δ}}_t$ and ${\text{Δ}}_{\text{ω}}$ are time and frequency resolutions respectively of $w\left(t\right)$ , then the uncertainty principle demands that ${\text{Δ}}_t{\text{Δ}}_{\text{ω}}\le 1/2$ [link] , [link] . Moreover, if the basis is orthonormal, the Balian-Low theorem implies either ${\text{Δ}}_t$ or ${\text{Δ}}_{\text{ω}}$ is infinite. Both ${\text{Δ}}_t$ and ${\text{Δ}}_{\text{ω}}$ can be controlled by the choice of $w\left(t\right)$ , but for any particular choice, there will be signals for which either the time or frequency resolution is not adequate. [link] shows the time-frequency tiles associated with the STFT basis for a narrow and widewindow, illustrating the inherent time-frequency trade-offs associated with this basis. Notice that the tiling schematic holds forseveral choices of windows (i.e., each figure represents all DSTFT bases with the particular time-frequency resolutioncharacteristic).

Tiling with the discrete two-band wavelet transform

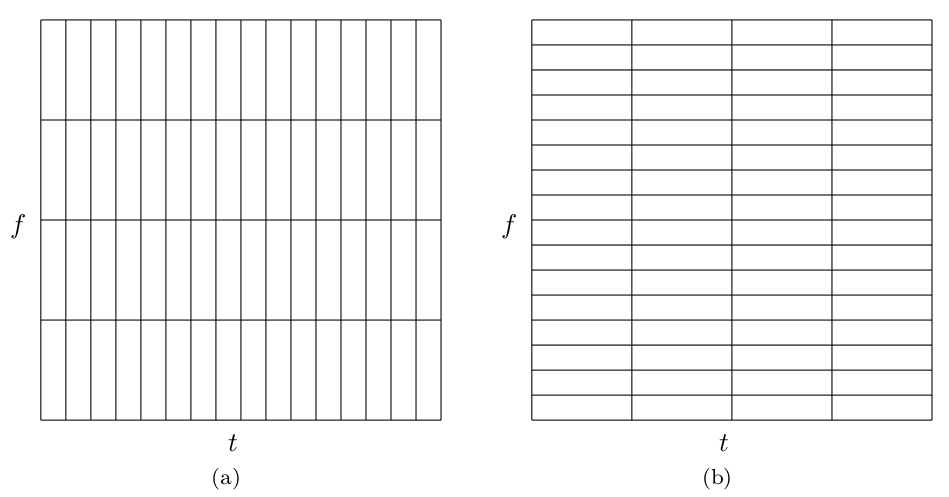
The discrete wavelet transform (DWT) is another signal-independent tiling of the time-frequency plane suited for signals where high frequency signal componentshave shorter duration than low frequency signal components. Time-frequency atoms for the DWT, $\left\{{\psi }_{j,k},\left(t\right)\right\}=\left\{2^{j/2},\psi ,(2^{j}t-k)\right\}$ , are obtained by translates and scales of the wavelet function $\psi \left(t\right)$ . One shrinks/stretches the wavelet to capture high-/low-frequency componentsof the signal. If these atoms form an orthonormal basis, then $x\left(t\right)={\sum }_{j,k}〈x,,,{\psi }_{j,k}〉{\psi }_{j,k}\left(t\right)$ . The DWT coefficients, $〈x,,,{\psi }_{j,k}〉$ , are a measure of the energy of the signal components located at $(2^{-j}k,2^j)$ in the time-frequency plane, giving yet another tiling of the time-frequency plane. As discussed in  Chapter: Filter Banks and the Discrete Wavelet Transform and Chapter: Filter Banks and Transmultiplexers , the DWT (for compactly supported wavelets) can be efficiently computedusing two-channel unitary FIR filter banks [link] . [link] shows the corresponding tiling description which illustrates time-frequency resolution propertiesof a DWT basis. If you look along the frequency (or scale) axis at someparticular time (translation), you can imagine seeing the frequency response of the filter bank as shown in [link] with the logarithmic bandwidth of each channel. Indeed, each horizontal strip inthe tiling of [link] corresponds to each channel, which in turn corresponds to a scale $j$ . The location of the tiles corresponding to each coefficient is shown in [link] . If at a particular scale, you imagine the translations along the $k$ axis, you see the construction of the components of a signal at that scale. Thismakes it obvious that at lower resolutions (smaller $j$ ) the translations are large and at higher resolutions the translations are small.