| << Chapter < Page | Chapter >> Page > |
We can think of an arithmetic sequence as a function on the domain of the natural numbers; it is a linear function because it has a constant rate of change. The common difference is the constant rate of change, or the slope of the function. We can construct the linear function if we know the slope and the vertical intercept.
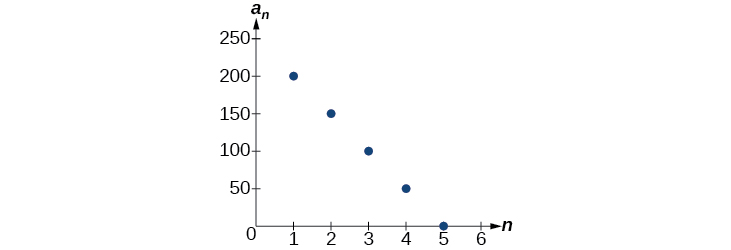
To find the y -intercept of the function, we can subtract the common difference from the first term of the sequence. Consider the following sequence.

The common difference is , so the sequence represents a linear function with a slope of . To find the -intercept, we subtract from . You can also find the -intercept by graphing the function and determining where a line that connects the points would intersect the vertical axis. The graph is shown in [link] .
Recall the slope-intercept form of a line is When dealing with sequences, we use in place of and in place of If we know the slope and vertical intercept of the function, we can substitute them for and in the slope-intercept form of a line. Substituting for the slope and for the vertical intercept, we get the following equation:
We do not need to find the vertical intercept to write an explicit formula for an arithmetic sequence. Another explicit formula for this sequence is , which simplifies to
An explicit formula for the term of an arithmetic sequence is given by
Given the first several terms for an arithmetic sequence, write an explicit formula.
Write an explicit formula for the arithmetic sequence.
The common difference can be found by subtracting the first term from the second term.
The common difference is 10. Substitute the common difference and the first term of the sequence into the formula and simplify.
Write an explicit formula for the following arithmetic sequence.
Explicit formulas can be used to determine the number of terms in a finite arithmetic sequence. We need to find the common difference, and then determine how many times the common difference must be added to the first term to obtain the final term of the sequence.
Given the first three terms and the last term of a finite arithmetic sequence, find the total number of terms.
Find the number of terms in the finite arithmetic sequence .
The common difference can be found by subtracting the first term from the second term.
The common difference is . Substitute the common difference and the initial term of the sequence into the term formula and simplify.
Substitute for and solve for
There are eight terms in the sequence.

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?