6.6 Surface integrals  (Page 2/27)

It follows from [link] that we can parameterize all cylinders of the form $x^2+y^2=R^2.$ If S is a cylinder given by equation $x^2+y^2=R^2,$ then a parameterization of S is

We can also find different types of surfaces given their parameterization, or we can find a parameterization when we are given a surface.

Describing a surface

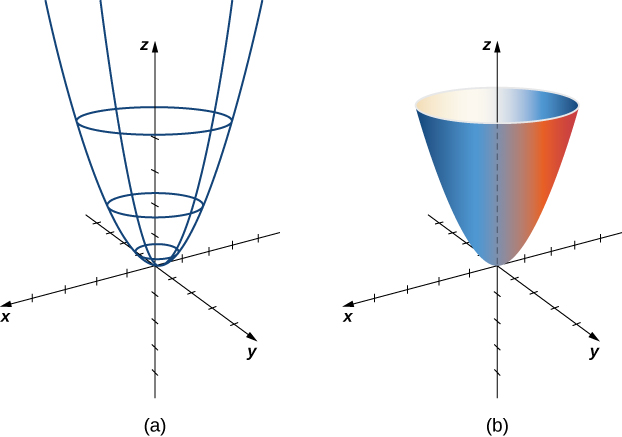
Describe surface S parameterized by

$\text{r}(u,v)=⟨u\text{cos}v,u\text{sin}v,u^2⟩,0\le u<\infty ,0\le v<2\pi .$

Notice that if u is held constant, then the resulting curve is a circle of radius u in plane $z=u.$ Therefore, as u increases, the radius of the resulting circle increases. If v is held constant, then the resulting curve is a vertical parabola. Therefore, we expect the surface to be an elliptic paraboloid. To confirm this, notice that

$\begin{array}{cc}\hfill x^2+y^2& ={\left(u\text{cos}v\right)}^2+{\left(u\text{sin}v\right)}^2\hfill \\ & =u^2{\text{cos}}^{2}v+u^2{\text{sin}}^{2}v\hfill \\ & =2u^2\hfill \\ & =2z.\hfill \end{array}$

Therefore, the surface is elliptic paraboloid $x^2+y^2=2z$ ( [link] ).

Got questions? Get instant answers now!

Got questions? Get instant answers now!

Finding a parameterization

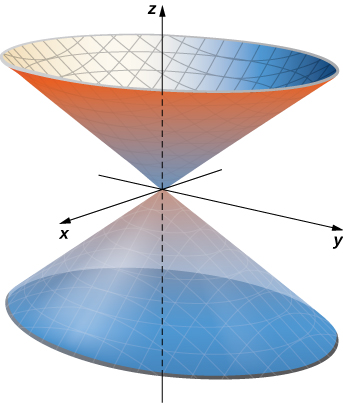
Give a parameterization of the cone $x^2+y^2=z^2$ lying on or above the plane $z=\mathrm{-2}.$

The horizontal cross-section of the cone at height $z=u$ is circle $x^2+y^2=u^2.$ Therefore, a point on the cone at height u has coordinates $\left(u\text{cos}v,u\text{sin}v,u\right)$ for angle v . Hence, a parameterization of the cone is $\text{r}(u,v)=⟨u\text{cos}v,u\text{sin}v,u⟩.$ Since we are not interested in the entire cone, only the portion on or above plane $z=\mathrm{-2},$ the parameter domain is given by $\mathrm{-2}<u<\infty ,0\le v<2\pi$ ( [link] ).

Got questions? Get instant answers now!

Got questions? Get instant answers now!

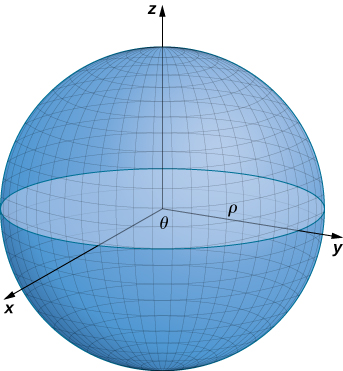
We have discussed parameterizations of various surfaces, but two important types of surfaces need a separate discussion: spheres and graphs of two-variable functions. To parameterize a sphere, it is easiest to use spherical coordinates. The sphere of radius $\rho$ centered at the origin is given by the parameterization

The idea of this parameterization is that as $\varphi$ sweeps downward from the positive z -axis, a circle of radius $\rho \text{sin}\varphi$ is traced out by letting $\theta$ run from 0 to $2\pi .$ To see this, let $\varphi$ be fixed. Then

This results in the desired circle ( [link] ).

Finally, to parameterize the graph of a two-variable function, we first let $z=f\left(x,y\right)$ be a function of two variables. The simplest parameterization of the graph of $f$ is $\text{r}(x,y)=⟨x,y,f\left(x,y\right)⟩,$ where x and y vary over the domain of $f$ ( [link] ). For example, the graph of $f(x,y)=x^{2}y$ can be parameterized by $\text{r}(x,y)=⟨x,y,x^{2}y⟩,$ where the parameters x and y vary over the domain of $f.$ If we only care about a piece of the graph of $f$ —say, the piece of the graph over rectangle $\left[1,3\right]\times \left[2,5\right]$ —then we can restrict the parameter domain to give this piece of the surface: