| << Chapter < Page | Chapter >> Page > |
Let S be a smooth orientable surface with parameterization For each point on the surface, vectors and lie in the tangent plane at that point. Vector is normal to the tangent plane at and is therefore normal to S at that point. Therefore, the choice of unit normal vector
gives an orientation of surface S .
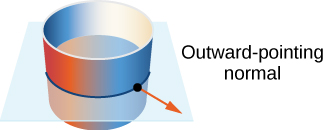
Give an orientation of cylinder
This surface has parameterization
The tangent vectors are and To get an orientation of the surface, we compute the unit normal vector
In this case, and therefore
An orientation of the cylinder is
Notice that all vectors are parallel to the xy -plane, which should be the case with vectors that are normal to the cylinder. Furthermore, all the vectors point outward, and therefore this is an outward orientation of the cylinder ( [link] ).
Since every curve has a “forward” and “backward” direction (or, in the case of a closed curve, a clockwise and counterclockwise direction), it is possible to give an orientation to any curve. Hence, it is possible to think of every curve as an oriented curve. This is not the case with surfaces, however. Some surfaces cannot be oriented; such surfaces are called nonorientable . Essentially, a surface can be oriented if the surface has an “inner” side and an “outer” side, or an “upward” side and a “downward” side. Some surfaces are twisted in such a fashion that there is no well-defined notion of an “inner” or “outer” side.
The classic example of a nonorientable surface is the Möbius strip. To create a Möbius strip, take a rectangular strip of paper, give the piece of paper a half-twist, and the glue the ends together ( [link] ). Because of the half-twist in the strip, the surface has no “outer” side or “inner” side. If you imagine placing a normal vector at a point on the strip and having the vector travel all the way around the band, then (because of the half-twist) the vector points in the opposite direction when it gets back to its original position. Therefore, the strip really only has one side.

Since some surfaces are nonorientable, it is not possible to define a vector surface integral on all piecewise smooth surfaces. This is in contrast to vector line integrals, which can be defined on any piecewise smooth curve.
With the idea of orientable surfaces in place, we are now ready to define a surface integral of a vector field . The definition is analogous to the definition of the flux of a vector field along a plane curve. Recall that if F is a two-dimensional vector field and C is a plane curve, then the definition of the flux of F along C involved chopping C into small pieces, choosing a point inside each piece, and calculating at the point (where N is the unit normal vector at the point). The definition of a surface integral of a vector field proceeds in the same fashion, except now we chop surface S into small pieces, choose a point in the small (two-dimensional) piece, and calculate at the point.

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?