| << Chapter < Page | Chapter >> Page > |
We have seen that a line integral is an integral over a path in a plane or in space. However, if we wish to integrate over a surface (a two-dimensional object) rather than a path (a one-dimensional object) in space, then we need a new kind of integral that can handle integration over objects in higher dimensions. We can extend the concept of a line integral to a surface integral to allow us to perform this integration.
Surface integrals are important for the same reasons that line integrals are important. They have many applications to physics and engineering, and they allow us to develop higher dimensional versions of the Fundamental Theorem of Calculus. In particular, surface integrals allow us to generalize Green’s theorem to higher dimensions, and they appear in some important theorems we discuss in later sections.
A surface integral is similar to a line integral, except the integration is done over a surface rather than a path. In this sense, surface integrals expand on our study of line integrals. Just as with line integrals, there are two kinds of surface integrals: a surface integral of a scalar-valued function and a surface integral of a vector field.
However, before we can integrate over a surface, we need to consider the surface itself. Recall that to calculate a scalar or vector line integral over curve C , we first need to parameterize C . In a similar way, to calculate a surface integral over surface S , we need to parameterize S . That is, we need a working concept of a parameterized surface (or a parametric surface ), in the same way that we already have a concept of a parameterized curve.
A parameterized surface is given by a description of the form
Notice that this parameterization involves two parameters, u and v , because a surface is two-dimensional, and therefore two variables are needed to trace out the surface. The parameters u and v vary over a region called the parameter domain, or parameter space —the set of points in the uv -plane that can be substituted into r . Each choice of u and v in the parameter domain gives a point on the surface, just as each choice of a parameter t gives a point on a parameterized curve. The entire surface is created by making all possible choices of u and v over the parameter domain.
Given a parameterization of surface the parameter domain of the parameterization is the set of points in the uv -plane that can be substituted into r .
Describe surface S parameterized by
To get an idea of the shape of the surface, we first plot some points. Since the parameter domain is all of we can choose any value for u and v and plot the corresponding point. If then so point (1, 0, 0) is on S . Similarly, points and are on S .
Although plotting points may give us an idea of the shape of the surface, we usually need quite a few points to see the shape. Since it is time-consuming to plot dozens or hundreds of points, we use another strategy. To visualize S , we visualize two families of curves that lie on S. In the first family of curves we hold u constant; in the second family of curves we hold v constant. This allows us to build a “skeleton” of the surface, thereby getting an idea of its shape.
First, suppose that u is a constant K . Then the curve traced out by the parameterization is which gives a vertical line that goes through point in the xy -plane.
Now suppose that v is a constant K. Then the curve traced out by the parameterization is which gives a circle in plane with radius 1 and center (0, 0, K ).
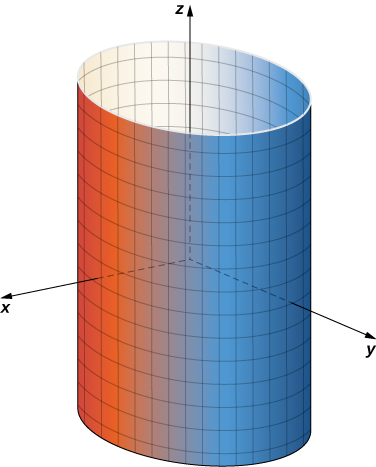
If u is held constant, then we get vertical lines; if v is held constant, then we get circles of radius 1 centered around the vertical line that goes through the origin. Therefore the surface traced out by the parameterization is cylinder ( [link] ).
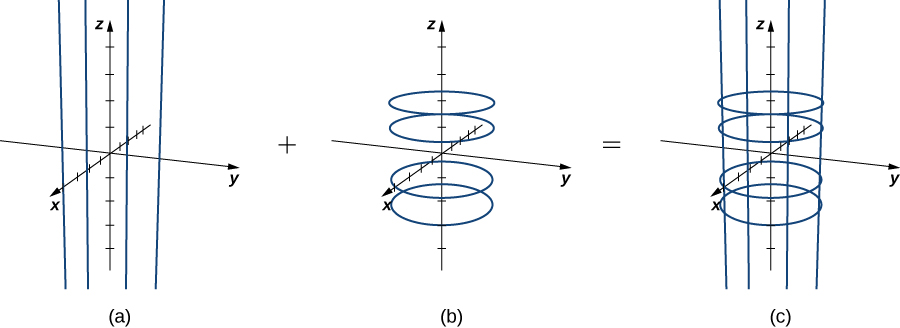
Notice that if and then so points from S do indeed lie on the cylinder. Conversely, each point on the cylinder is contained in some circle for some k , and therefore each point on the cylinder is contained in the parameterized surface ( [link] ).

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?