| << Chapter < Page | Chapter >> Page > |
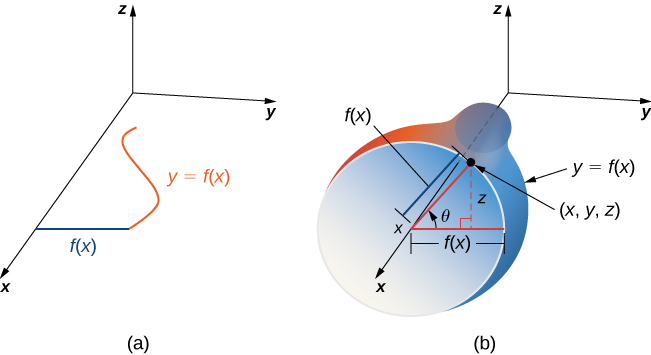
In addition to parameterizing surfaces given by equations or standard geometric shapes such as cones and spheres, we can also parameterize surfaces of revolution. Therefore, we can calculate the surface area of a surface of revolution by using the same techniques. Let be a positive single-variable function on the domain and let S be the surface obtained by rotating about the x -axis ( [link] ). Let be the angle of rotation. Then, S can be parameterized with parameters x and by
Find the area of the surface of revolution obtained by rotating about the x -axis ( [link] ).
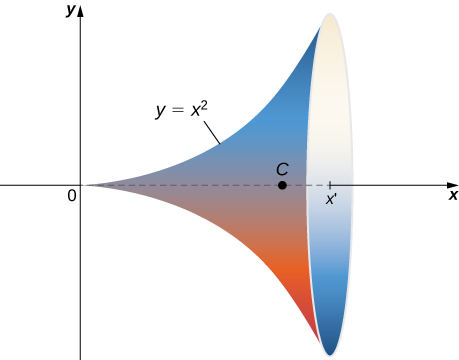
This surface has parameterization
The tangent vectors are Therefore,
and
The area of the surface of revolution is
Use [link] to find the area of the surface of revolution obtained by rotating curve about the x -axis.
Now that we can parameterize surfaces and we can calculate their surface areas, we are able to define surface integrals. First, let’s look at the surface integral of a scalar-valued function. Informally, the surface integral of a scalar-valued function is an analog of a scalar line integral in one higher dimension. The domain of integration of a scalar line integral is a parameterized curve (a one-dimensional object); the domain of integration of a scalar surface integral is a parameterized surface (a two-dimensional object). Therefore, the definition of a surface integral follows the definition of a line integral quite closely. For scalar line integrals, we chopped the domain curve into tiny pieces, chose a point in each piece, computed the function at that point, and took a limit of the corresponding Riemann sum. For scalar surface integrals, we chop the domain region (no longer a curve) into tiny pieces and proceed in the same fashion.
Let S be a piecewise smooth surface with parameterization with parameter domain D and let be a function with a domain that contains S. For now, assume the parameter domain D is a rectangle, but we can extend the basic logic of how we proceed to any parameter domain (the choice of a rectangle is simply to make the notation more manageable). Divide rectangle D into subrectangles with horizontal width and vertical length Suppose that i ranges from 1 to m and j ranges from 1 to n so that D is subdivided into mn rectangles. This division of D into subrectangles gives a corresponding division of S into pieces Choose point in each piece evaluate at , and multiply by area to form the Riemann sum

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?