| << Chapter < Page | Chapter >> Page > |
Applying the linearity property [link] and the result of Exercise [link] gives
Thus, the spectrum of a sine wave is a pair of functions with opposite signs, located symmetrically about zero frequency. The corresponding magnitude spectrum,shown in [link] , is at the heart of one importantinterpretation of the Fourier transform: it shows the frequency content of any signal by displayingwhich frequencies are present (and which frequencies are absent) from the waveform. For example, [link] (a) shows the magnitude spectrum of a real-valued signal . This can be interpreted as saying that contains (or is made up of) “all the frequencies” up to Hz, and that it contains no sinusoids with higher frequency. Similarly,the modulated signal in [link] (b) contains all positive frequencies between and , and no others.
Note that the Fourier transform in [link] is purely imaginary, as it must be because is odd (see [link] ). The phase spectrum is a flat line at because of the factor .
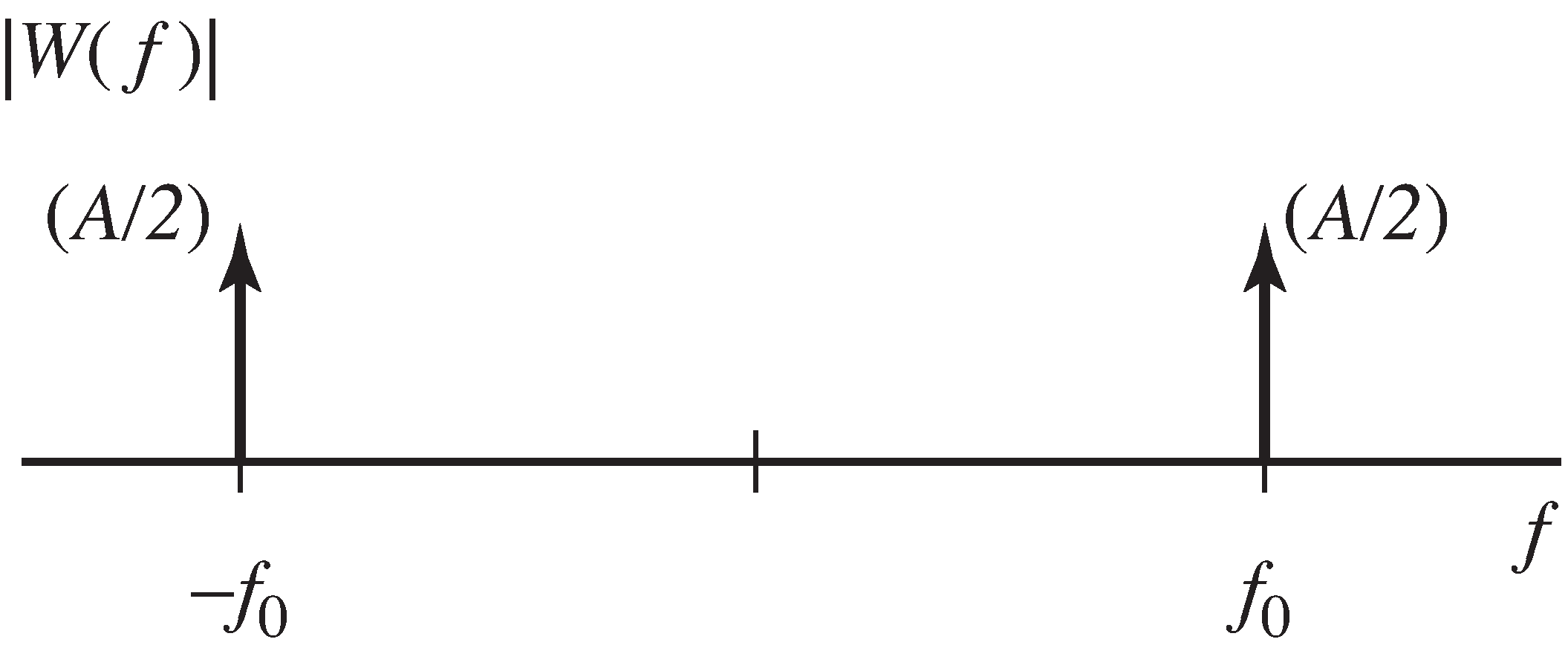

Let . What is the corresponding time function?
Suppose that a system has impulse response , and that the input consists of a sum of three impulses occurring at times , , and , with amplitudes , , and (for example, the signal of [link] ). By linearity of the Fourier transform, property [link] , the output is a superpositionof the outputs due to each of the input pulses. The output due to the first impulse is , which is the impulse response scaled by the size of the input and shifted to beginwhen the first input pulse arrives. Similarly, the outputs to the second and thirdinput impulses are and , respectively, and the complete output is the sum .
Now suppose that the input is a continuous function . At any time instant , the input can be thought of as consisting of an impulse scaled by the amplitude , and the corresponding output will be , which is the impulse response scaled by thesize of the input and shifted to begin at time . The complete output is then given by integrating over all

Notification Switch
Would you like to follow the 'Software receiver design' conversation and receive update notifications?