| << Chapter < Page | Chapter >> Page > |

The discrete time counterpart of is the (discrete) delta function
While there are a few subtleties (i.e., differences) between
and
, for the most part they act analogously.
For example, the program
specdelta.m calculates the
spectrum of the (discrete) delta function.
time=2;
% length of timeTs=1/100; % time interval between samples
t=Ts:Ts:time; % create time vectorx=zeros(size(t)); % create signal of all zeros
x(1)=1;% delta function
plotspec(x,Ts) % draw waveform and spectrum
specdelta.m plots the spectrum of a delta function
(download file)
The output of
specdelta.m is shown in
[link] .
As expected from
[link] , the magnitude spectrum of
the delta function is equal to 1 at all frequencies.
Calculate the Fourier transform of from the definition. Now calculate it using the time shift property [link] . Are they the same?Hint: They had better be.
Use the definition of the IFT [link] to show that
Mimic the code in
specdelta.m to find the spectrum
of the discrete delta function when:
x . Try
x[10]=1 ,
x[100]=1 ,
and
x[110]=1 . How do the spectra differ?
Can you use the time shift property
[link] to explain what you see?x .
Try
x[1]=10 ,
x[10]=3 ,
and
x[110]= 0.1 . How do the spectra differ?
Can you use the linearity property
[link] to explain what you see?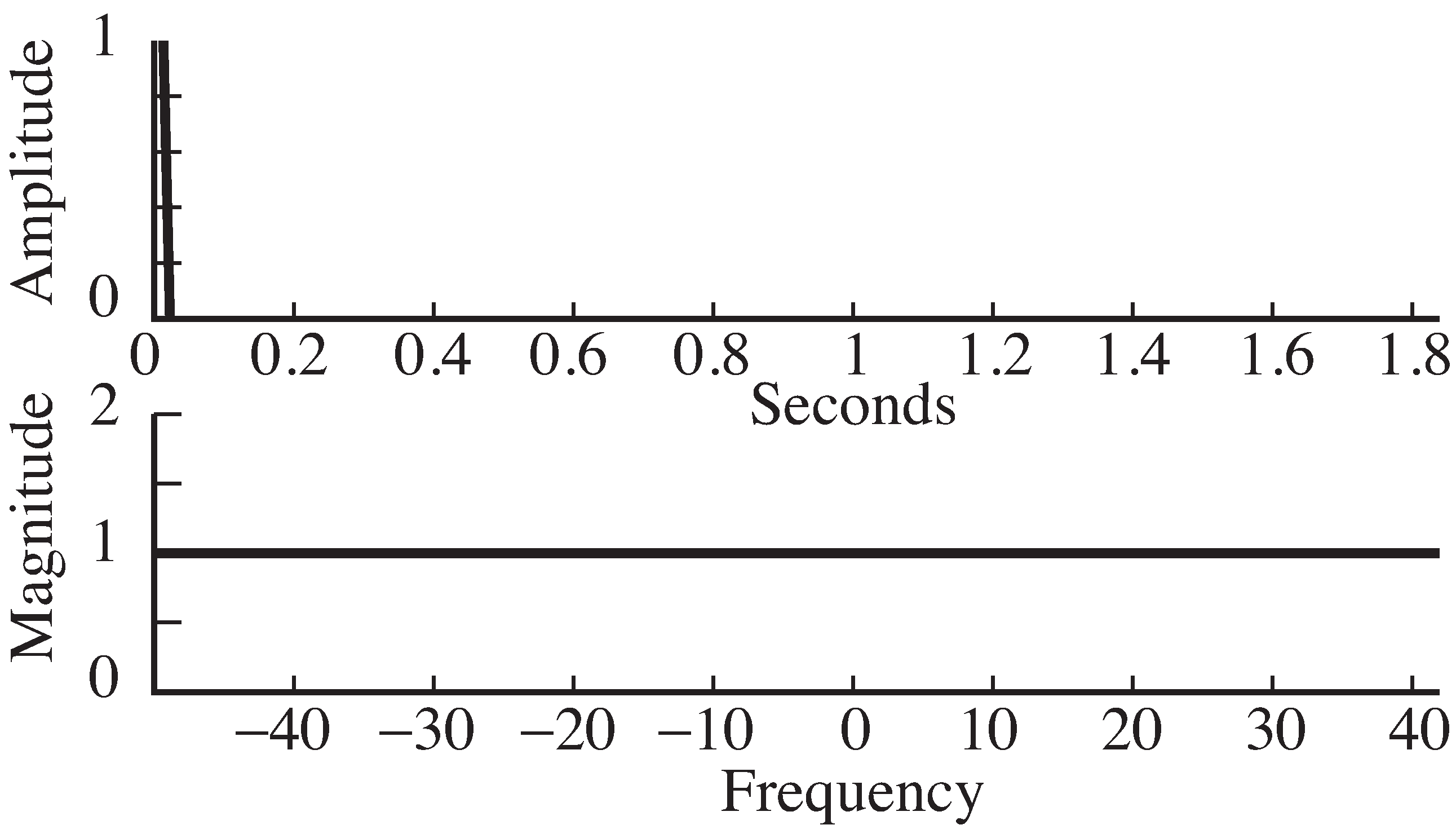
Mimic the code in
specdelta.m to find the magnitude spectrum
of the discrete delta function when:
x . Try
x[10]=1 ,
x[100]=1 ,
and
x[110]=1 . How do the spectra differ?
Can you use the time shift property
[link] to explain what you see?x .
Try
x[1]=10 ,
x[10]=3 ,
and
x[110]= 0.1 . How do the spectra differ?
Can you use the linearity property
[link] to explain what you see?Modify the code in
specdelta.m to find the phase spectrum
of a signal that consists of a delta function when the nonzero termis located at the start (
x(1)=1 ), the middle (
x(100)=1 )
and at the end (
x(200)=1 ).
Mimic the code in
specdelta.m to find the spectrum
of a train of equally spaced pulses. For instance,
x(1:20:end)=1 spaces the pulses 20 samples apart, and
x(1:25:end)=1 places the pulses 25 samples apart.
In [link] , the spectrum of a sinusoid was shown to consist of two symmetrical spikes in the frequency domain,(recall [link] ). The next example shows why this is true by explicitly taking the Fouriertransform.
Let , and use Euler's identity [link] to rewrite as

Notification Switch
Would you like to follow the 'Software receiver design' conversation and receive update notifications?