0.3 Modelling corruption (Page 8/11)

Page 8 / 11

This integral defines the convolution operator $*$ and provides a way of finding the output $y (t)$ of any linear system, given its impulse response $h (t)$ and the input $x (t)$ .

M atlab has several functions that simplify the numerical evaluation of convolutions. The most obvious of these is conv , which is used in convolex.m to calculate the convolution of an input x (consisting of two delta functions at times $t = 1$ and $t = 3$ ) and a system with impulse response h that is an exponential pulse. The convolution gives the output of the system.

Ts=1/100; time=10;             % sampling interval and total time
t=0:Ts:time;                   % create time vectorh=exp(-t);                     % define impulse response
x=zeros(size(t));              % input is sum of two delta functions...x(1/Ts)=3; x(3/Ts)=2;          % ...at times t=1 and t=3
y=conv(h,x);                   % do convolution and plotsubplot(3,1,1), plot(t,x)
subplot(3,1,2), plot(t,h)subplot(3,1,3), plot(t,y(1:length(t)))

convolex.m  example of numerical convolution
(download file)

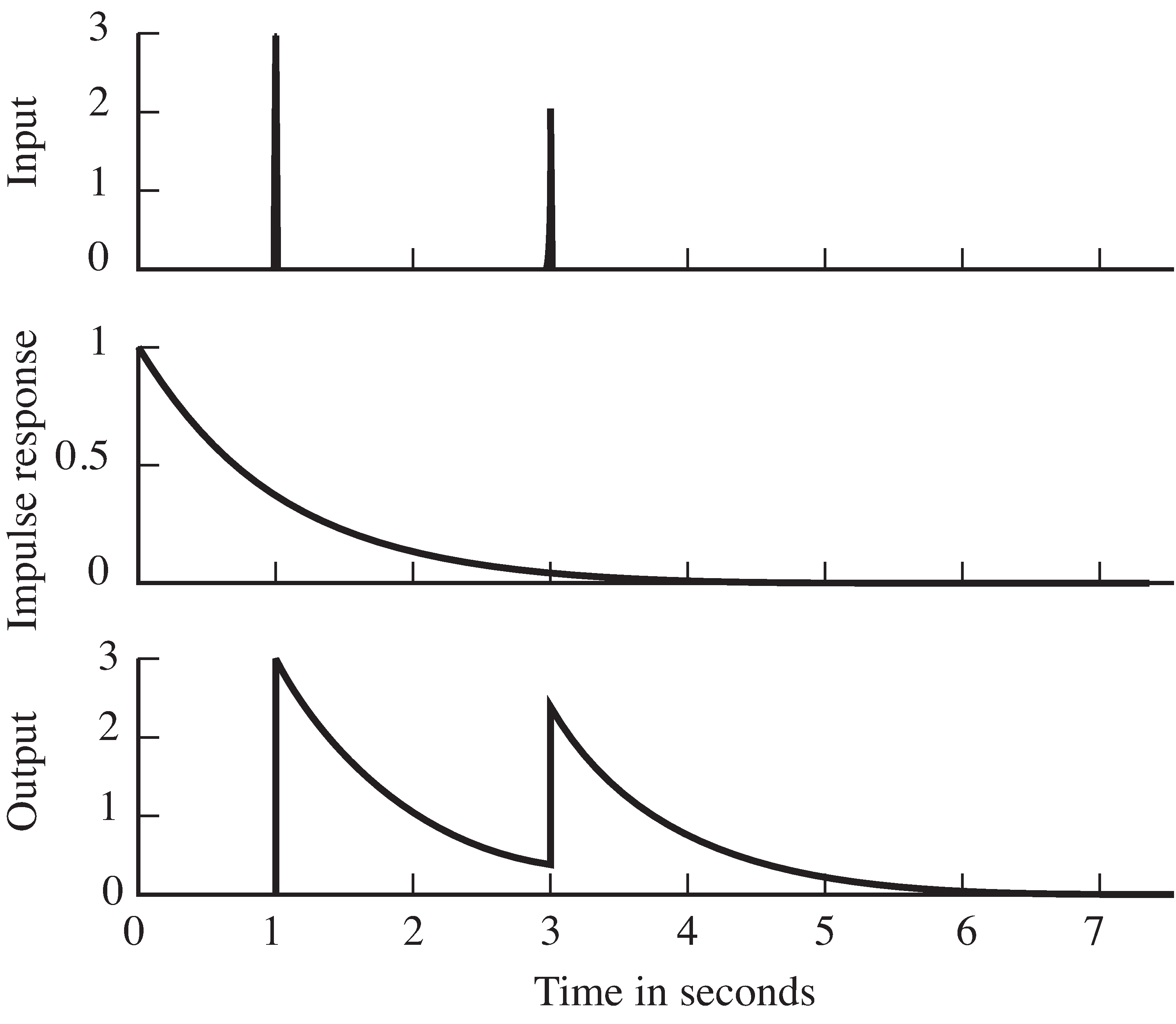
The convolution of the input (the top plot) with the impulse response of the system (the middle plot) gives the output in the bottom plot.

[link] shows the input to the system in the top plot,the impulse response in the middle plot, and the output of the system in the bottom plot. Nothing happens before time $t = 1$ , and the output is zero. When the first spike occurs,the system responds by jumping to 3 and then decaying slowly at a rate dictated by the shape of $h (t)$ . The decay continues smoothly until time $t = 3$ , when the second spike enters. At this point, the output jumps up by 2, andis the sum of the response to the second spike, plus the remainder of the response to the first spike. Since there are no more inputs,the output slowly dies away.

Suppose that the impulse response $h (t)$ of a linear system is the exponential pulse

h (t) = \{\begin{matrix} e^{- t} & t \geq 0 \\ 0 & t < 0 \end{matrix} .)

Suppose that the input to the system is $3 δ (t - 1) + 2 δ (t - 3)$ . Use the definition of convolution [link] to show that the output is $3 h (t - 1) + 2 h (t - 3)$ , where

h (t - t_{0}) = [\begin{matrix} e^{- t + t_{0}} & t \geq t_{0} \\ 0 & t < t_{0} \end{matrix}] .

How does your answer compare to [link] ?

Suppose that a system has an impulse response that is an exponential pulse. Mimic the code in convolex.m to find its output when the input is a white noise (recall specnoise.m ).

Mimic the code in convolex.m to find the output of a system when the input is an exponential pulse and theimpulse response is a sum of two delta functions at times $t = 1$ and $t = 3$ .

The next two problems show that linear filters commute with differentiation, and with each other.

Use the definition to show that convolution is commutative (i.e., that $w_{1} (t) * w_{2} (t) = w_{2} (t) * w_{1} (t)$ ). Hint: Apply the change of variables $τ = t - λ$ in [link] .

Suppose a filter has impulse response $h (t)$ . When the input is $x (t)$ , the output is $y (t)$ . If the input is $x_{d} (t) = \frac{\partial x (t)}{\partial t}$ , the output is $y_{d} (t)$ . Show that $y_{d} (t)$ is the derivative of $y (t)$ . Hint: Use [link] and the result of Exercise [link] .

Let $w (t) = Π (t)$ be the rectangular pulse of [link] . What is $w (t) * w (t)$ ? Hint: A pulse shaped like a triangle.

Redo Exercise [link] numerically by suitably modifying convolex.m . Let $T = 1.5$ seconds.

<< Chapter < Page Page > Chapter >>

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Software receiver design. OpenStax CNX. Aug 13, 2013 Download for free at http://cnx.org/content/col11510/1.3

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Software receiver design' conversation and receive update notifications?

Ask

	8 Physiotherapy MMT Review By Rhodes Start Flashcards
	20 Biology 20 Phylogenies the History of Life MCQ By OpenStax Start Quiz
	Chemistry Final By Briana Hamilton Start Flashcards
	Tournament Director Quiz By Eddie Unverzagt Start Quiz
©flickr: Luis	Chemistry Final Review By Madison Christian Start Exam
	4 Neuroanatomy 04 Spinal Cord Brain Stem By Stephen Voron Start Quiz
	20 Sociology 20 Population Urbanization Environment By OpenStax Start Quiz
	Economy Foundations By Robert Murphy Start Test
©flickr: Gage	How well do you know Ross Lynch? By Brianna Beck Start Quiz
	Microbiology Practice Test By Sandhills MLT Start Test