0.6 Regularity, moments, and wavelet system design  (Page 9/13)

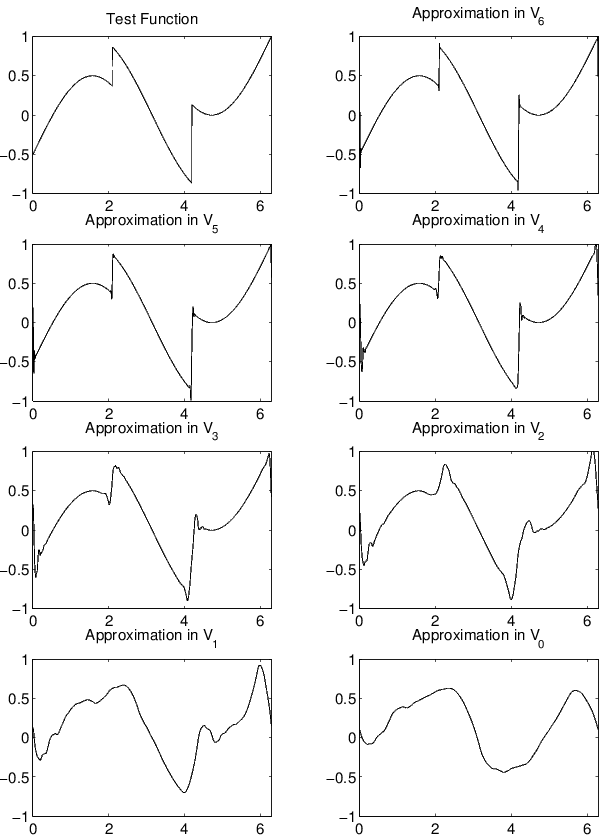
An illustration of the effects of these approximations on a signal is shown in [link] where a signal with a very smooth component (a sinusoid) and a discontinuous component (a square wave) is expanded in awavelet series using samples as the high resolution scaling function coefficients. Notice the effects of projecting onto lower and lowerresolution scales.

If we consider a wavelet system where the same number of scaling function and wavelet moments are set zero and this number is as large as possible,then the following is true [link] , [link] :

Theorem 27 If $m\left(\ell \right)=m_1\left(\ell \right)=0$ for $\ell =1,2,\cdots ,L$ and $m_1\left(0\right)=0$ , then the $L^2$ error is

where $C_3$ is a constant independent of $j$ and $L$ , but dependent on $f\left(t\right)$ and the wavelet system.

Here we see that for this wavelet system called a Coifman wavelet system, that using samples as the inner product expansion coefficients is anexcellent approximation. This justifies that using samples of a signal as input to a filter bank gives a proper wavelet analysis. This approximationis also illustrated in [link] and in [link] .

Coiflets and related wavelet systems

From the previous approximation theorems, we see that a combination of zero wavelet and zero scaling function moments used with samples of thesignal may give superior results to wavelets with only zero wavelet moments. Not only does forcing zero scaling function moments give abetter approximation of the expansion coefficients by samples, it often causesthe scaling function to be more symmetric. Indeed, that characteristic may be more important than the sample approximation in certainapplications.

Daubechies considered the design of these wavelets which were suggested by Coifman [link] , [link] , [link] . Gopinath [link] , [link] and Wells [link] , [link] show how zero scaling function moments give a better approximation of high-resolution scaling coefficients by samples. Tianand Wells [link] , [link] have also designed biorthogonal systems with mixed zero moments with very interesting properties.

The Coifman wavelet system (Daubechies named the basis functions “coiflets") is an orthonormal multiresolution wavelet system with

This definition imposes the requirement that there be at least $L-1$ zero scaling function moments and at least $L-1$ wavelet moments in addition to the one zero moment of $m_1\left(0\right)$ required by orthogonality. This system is said to be of order or degree $L$ and sometime has the additional requirement that the length of the scaling function filter $h\left(n\right)$ , which is denoted $N$ , is minimum [link] , [link] . In the design of these coiflets, one obtains more total zero moments than $N/2-1$ . This was first noted by Beylkin, et al [link] . The length-4 wavelet systemhas only one degree of freedom, so it cannot have both a scaling function moment and wavelet moment of zero (see [link] ). Tian [link] , [link] has derived formulas for four length-6 coiflets. These are:

or

or

or