0.6 Regularity, moments, and wavelet system design  (Page 6/13)

The Daubechies coefficients are obtained by maximizing the number of moments that are zero. This gives regular scaling functions and wavelets,but it is possible to use the degrees of

freedom to maximize the differentiability of $\phi \left(t\right)$ rather than maximize the zero moments. This is not easily parameterized, and it gives only slightly greatersmoothness than the Daubechies system [link] .

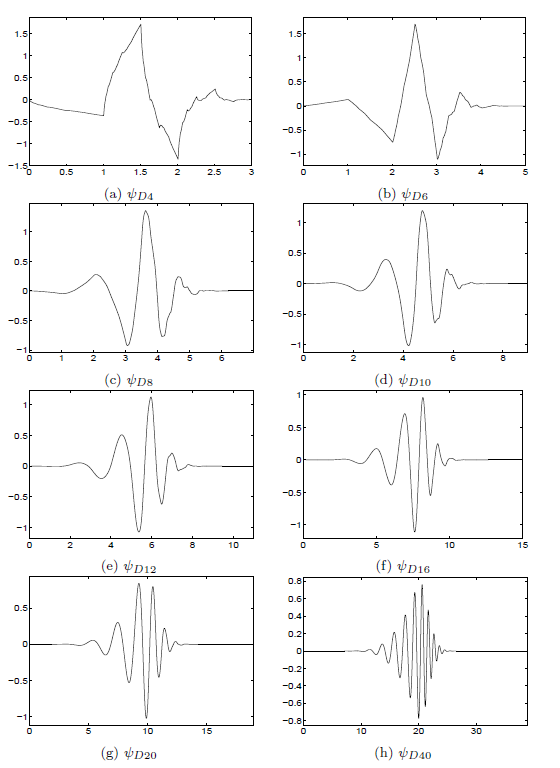
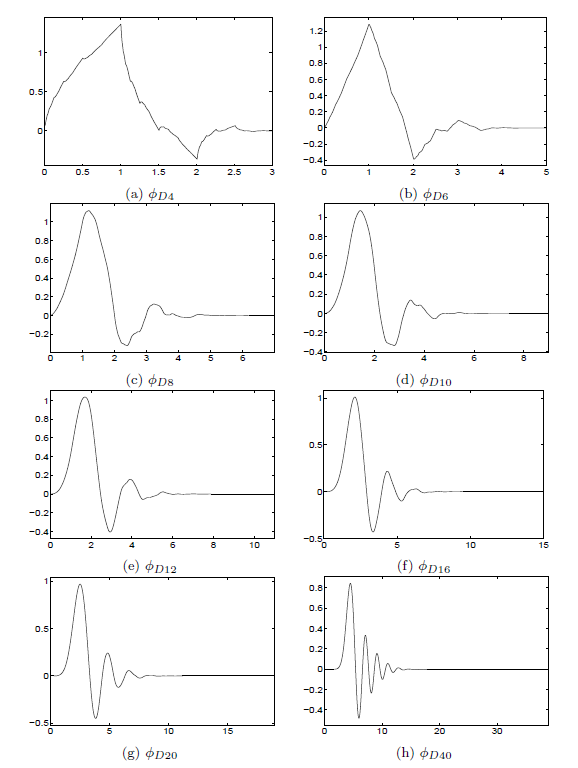
Examples of Daubechies scaling functions resulting from choosing different factors in the spectral factorization of ${\left|H\left(\omega \right)\right|}^2$ in [link] can be found in [link] .

Non-maximal regularity wavelet design

If the length of the scaling coefficient filter is longer than twice the desired regularity, i.e., $N>2K$ , then the parameterization of [link] should be used and the coefficients in the polynomial $R\left(y\right)$ must be determined. One interesting possibility is that of designing a system that has one or more zeros of $H\left(\omega \right)$ between $\omega =\pi /2$ and $\omega =\pi$ with the remaining zeros at $\pi$ to contribute to the regularity. This will give better frequency separation in the filter bankin exchange for reduced regularity and lower degree polynomial representation.

If a zero of $H\left(\omega \right)$ is set at $\omega ={\omega }_0$ , then the conditions of

are imposed with those in [link] , giving a set of linear simultaneous equations that can be solved to find the scaling coefficients $h\left(n\right)$ .

A powerful design system based on a Remez exchange algorithm allows the design of an orthogonal wavelet system that has a specified regularity andan optimal Chebyshev behavior in the stopband of $H\left(\omega \right)$ . This and a variation that uses a constrained least square criterion [link] is described in [link] and another Chebyshev design in [link] .

An alternative approach is to design the wavelet system by setting an optimization criterion and using a general constrained optimizationroutine, such as that in the Matlab optimization toolbox, to design the $h\left(n\right)$ with the existence and orthogonality conditions as constraints. This approach was used to generate many of the filters described in [link] . Jun Tian used a Newton's method [link] , [link] to design wavelet systems with zero moments.

Relation of zero wavelet moments to smoothness

We see from  [link] and [link] that there is a relationship between zero wavelet moments and smoothness, but it is nottight. Although in practical application the degree of differentiability may not be the most important measure, it is an important theoreticalquestion that should be addressed before application questions can be properly posed.

First we must define smoothness. From the mathematical point of view, smoothness is essentially the same as differentiability and there are atleast two ways to pose that measure. The first is local (the Hölder measure) and the second is global (the Sobolev measure).Numerical algorithms for estimating the measures in the wavelet setting have been developed by Rioul [link] and Heller and Wells [link] , [link] for the Hölder and Sobolev measures respectively.

Definition 1 (Hölder continuity) Let $\phi :\mathrm{I}\mathrm{R}\to \text{C}$ and let 0<α<1. Then the function φ is Hölder continuous of order α if there exists a constant c such that