| << Chapter < Page | Chapter >> Page > |
While the moments of the wavelets give information about flatness of and smoothness of , the moments of and are measures of the “localization" and symmetry characteristics of the scaling function and, therefore, the wavelet transform. We know from [link] that and, after normalization, that . Using [link] , one can show [link] that for , we have
This can be seen in [link] . A generalization of this result has been developed by Johnson [link] and is given in [link] through [link] .
A more general picture of the effects of zero moments can be seen by next considering two approximations. Indeed, this analysis gives a veryimportant insight into the effects of zero moments. The mixture of zero scaling function moments with other specifications is addressed laterin [link] .
The orthogonal projection of a signal on the scaling function subspace is given and denoted by
which gives the component of which is in and which is the best least squares approximation to in .
As given in [link] , the moment of is defined as
We can now state an important relation of the projection [link] as an approximation to in terms of the number of zero wavelet moments and the scale.
Theorem 25 If for then the error is
where is a constant independent of and but dependent on and the wavelet system [link] , [link] .
This states that at any given scale, the projection of the signal on the subspace at that scale approaches the function itself as the numberof zero wavelet moments (and the length of the scaling filter) goes to infinity. It also states that for any given length, the projection goesto the function as the scale goes to infinity. These approximations converge exponentially fast. This projection is illustrated in [link] .
A second approximation involves using the samples of as the inner product coefficients in the wavelet expansion of in [link] . We denote this sampling approximation by
and the scaling function moment by
and can state [link] the following
Theorem 26 If for then the error is
where is a constant independent of and but dependent on and the wavelet system.
This is a similar approximation or convergence result to the previous theorem but relates the projection of on a -scale subspace to the sampling approximation in that same subspace. These approximationsare illustrated in [link] .
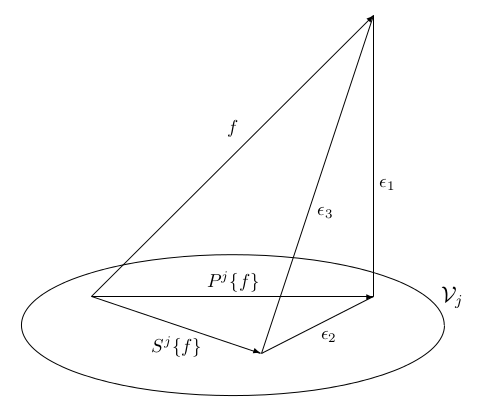
This “vector space" illustration shows the nature and relationships of the two types of approximations. The use of samples as inner productsis an approximation within the expansion subspace . The use of a finite expansion to represent a signal is an approximation from onto the subspace . Theorems [link] and [link] show the nature of those approximations, which, for wavelets, is very good.

Notification Switch
Would you like to follow the 'Wavelets and wavelet transforms' conversation and receive update notifications?