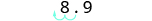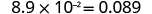-
Home
- Elementary algebra
- Polynomials
- Integer exponents and scientific
The steps are summarized below.
Convert scientific notation to decimal form.
To convert scientific notation to decimal form:
- Determine the exponent,
, on the factor 10.
- Move the decimal
places, adding zeros if needed.
- If the exponent is positive, move the decimal point
places to the right.
- If the exponent is negative, move the decimal point
places to the left.
- Check.
Multiply and divide using scientific notation
Astronomers use very large numbers to describe distances in the universe and ages of stars and planets. Chemists use very small numbers to describe the size of an atom or the charge on an electron. When scientists perform calculations with very large or very small numbers, they use scientific notation. Scientific notation provides a way for the calculations to be done without writing a lot of zeros. We will see how the Properties of Exponents are used to multiply and divide numbers in scientific notation.
Key concepts
-
Property of Negative Exponents
- If
is a positive integer and
, then
-
Quotient to a Negative Exponent
- If
are real numbers,
and
is an integer , then
-
To convert a decimal to scientific notation:
- Move the decimal point so that the first factor is greater than or equal to 1 but less than 10.
- Count the number of decimal places,
, that the decimal point was moved.
- Write the number as a product with a power of 10. If the original number is:
- greater than 1, the power of 10 will be
- between 0 and 1, the power of 10 will be
- Check.
-
To convert scientific notation to decimal form:
- Determine the exponent,
, on the factor 10.
- Move the decimal
places, adding zeros if needed.
- If the exponent is positive, move the decimal point
places to the right.
- If the exponent is negative, move the decimal point
places to the left.
- Check.
Questions & Answers
evolutionary history and relationship of an organism or group of organisms
AI-Robot
the study of living organisms and their interactions with one another and their environments
AI-Robot
HOW CAN MAN ORGAN FUNCTION
the diagram of the digestive system
allimentary cannel
Ogenrwot
They formed in two ways first when one sperm and one egg are splited by mitosis or two sperm and two eggs join together
Oluwatobi
Genetics is the study of heredity
Misack
how does twins formed?
Misack
discuss biological phenomenon and provide pieces of evidence to show that it was responsible for the formation of eukaryotic organelles
the study of living organisms and their interactions with one another and their environment.
Wine
discuss the biological phenomenon and provide pieces of evidence to show that it was responsible for the formation of eukaryotic organelles in an essay form
list any five characteristics of the blood cells
Shaker
lack electricity and its more savely than electronic microscope because its naturally by using of light
advantage of electronic microscope is easily and clearly while disadvantage is dangerous because its electronic. advantage of light microscope is savely and naturally by sun while disadvantage is not easily,means its not sharp and not clear
Abdullahi
cell theory state that every organisms composed of one or more cell,cell is the basic unit of life
Abdullahi
is like gone fail us
DENG
cells is the basic structure and functions of all living things
Ramadan
is organisms that are similar into groups called tara
Yamosa
in what situation (s) would be the use of a scanning electron microscope be ideal and why?
A scanning electron microscope (SEM) is ideal for situations requiring high-resolution imaging of surfaces. It is commonly used in materials science, biology, and geology to examine the topography and composition of samples at a nanoscale level. SEM is particularly useful for studying fine details,
Hilary
Got questions? Join the online conversation and get instant answers!
Source:
OpenStax, Elementary algebra. OpenStax CNX. Jan 18, 2017 Download for free at http://cnx.org/content/col12116/1.2
Google Play and the Google Play logo are trademarks of Google Inc.