| << Chapter < Page | Chapter >> Page > |
Remember working with place value for whole numbers and decimals? Our number system is based on powers of 10. We use tens, hundreds, thousands, and so on. Our decimal numbers are also based on powers of tens—tenths, hundredths, thousandths, and so on. Consider the numbers 4,000 and . We know that 4,000 means and 0.004 means .
If we write the 1000 as a power of ten in exponential form, we can rewrite these numbers in this way:
When a number is written as a product of two numbers, where the first factor is a number greater than or equal to one but less than 10, and the second factor is a power of 10 written in exponential form, it is said to be in scientific notation.
A number is expressed in scientific notation when it is of the form
It is customary in scientific notation to use as the multiplication sign, even though we avoid using this sign elsewhere in algebra.
If we look at what happened to the decimal point, we can see a method to easily convert from decimal notation to scientific notation .

In both cases, the decimal was moved 3 places to get the first factor between 1 and 10.
Write in scientific notation:
The original number, , is between 0 and 1 so we will have a negative power of 10.
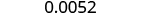 | |
| Move the decimal point to get 5.2, a number between 1 and 10. |
 |
| Count the number of decimal places the point was moved. |
 |
| Write as a product with a power of 10. |
 |
| Check. | |
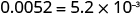 |
How can we convert from scientific notation to decimal form? Let’s look at two numbers written in scientific notation and see.
If we look at the location of the decimal point, we can see an easy method to convert a number from scientific notation to decimal form.
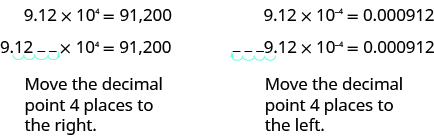
In both cases the decimal point moved 4 places. When the exponent was positive, the decimal moved to the right. When the exponent was negative, the decimal point moved to the left.

Notification Switch
Would you like to follow the 'Elementary algebra' conversation and receive update notifications?