| << Chapter < Page | Chapter >> Page > |
For the following exercises, use function composition to verify that and are inverse functions.
For the following exercises, use a graphing utility to determine whether each function is one-to-one.
For the following exercises, determine whether the graph represents a one-to-one function.
For the following exercises, use the graph of shown in [link] .
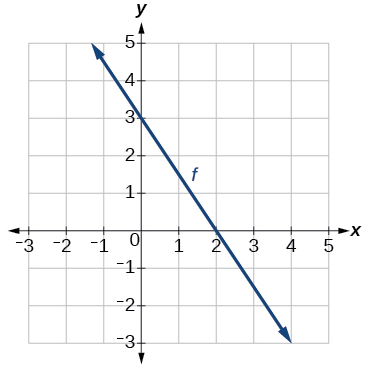
For the following exercises, use the graph of the one-to-one function shown in [link] .
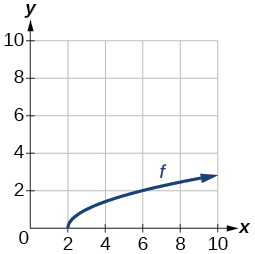
If the complete graph of is shown, find the range of
For the following exercises, evaluate or solve, assuming that the function is one-to-one.
For the following exercises, use the values listed in [link] to evaluate or solve.
| 0 | 8 |
| 1 | 0 |
| 2 | 7 |
| 3 | 4 |
| 4 | 2 |
| 5 | 6 |
| 6 | 5 |
| 7 | 3 |
| 8 | 9 |
| 9 | 1 |
Use the tabular representation of in [link] to create a table for
| 3 | 6 | 9 | 13 | 14 | |
| 1 | 4 | 7 | 12 | 16 |
| 1 | 4 | 7 | 12 | 16 | |
| 3 | 6 | 9 | 13 | 14 |
For the following exercises, find the inverse function. Then, graph the function and its inverse.
Find the inverse function of Use a graphing utility to find its domain and range. Write the domain and range in interval notation.
To convert from degrees Celsius to degrees Fahrenheit, we use the formula Find the inverse function, if it exists, and explain its meaning.
Given the Fahrenheit temperature, this formula allows you to calculate the Celsius temperature.
The circumference of a circle is a function of its radius given by Express the radius of a circle as a function of its circumference. Call this function Find and interpret its meaning.
A car travels at a constant speed of 50 miles per hour. The distance the car travels in miles is a function of time, in hours given by Find the inverse function by expressing the time of travel in terms of the distance traveled. Call this function Find and interpret its meaning.
The time for the car to travel 180 miles is 3.6 hours.
For the following exercises, determine whether the relation is a function.
for the independent variable and the dependent variable
not a function
Is the graph in [link] a function?
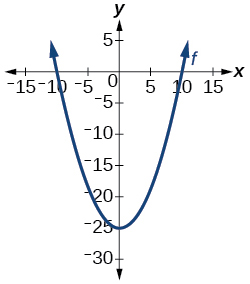
For the following exercises, evaluate the function at the indicated values:
For the following exercises, determine whether the functions are one-to-one.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?