| << Chapter < Page | Chapter >> Page > |
The domain of function is and the range of function is Find the domain and range of the inverse function.
The domain of function is and the range of function is
Once we have a one-to-one function, we can evaluate its inverse at specific inverse function inputs or construct a complete representation of the inverse function in many cases.
Suppose we want to find the inverse of a function represented in table form. Remember that the domain of a function is the range of the inverse and the range of the function is the domain of the inverse. So we need to interchange the domain and range.
Each row (or column) of inputs becomes the row (or column) of outputs for the inverse function. Similarly, each row (or column) of outputs becomes the row (or column) of inputs for the inverse function.
A function is given in [link] , showing distance in miles that a car has traveled in minutes. Find and interpret
| 30 | 50 | 70 | 90 | |
| 20 | 40 | 60 | 70 |
The inverse function takes an output of and returns an input for So in the expression 70 is an output value of the original function, representing 70 miles. The inverse will return the corresponding input of the original function 90 minutes, so The interpretation of this is that, to drive 70 miles, it took 90 minutes.
Alternatively, recall that the definition of the inverse was that if then By this definition, if we are given then we are looking for a value so that In this case, we are looking for a so that which is when
Using [link] , find and interpret (a) and (b)
| 30 | 50 | 60 | 70 | 90 | |
| 20 | 40 | 50 | 60 | 70 |
We saw in Functions and Function Notation that the domain of a function can be read by observing the horizontal extent of its graph. We find the domain of the inverse function by observing the vertical extent of the graph of the original function, because this corresponds to the horizontal extent of the inverse function. Similarly, we find the range of the inverse function by observing the horizontal extent of the graph of the original function, as this is the vertical extent of the inverse function. If we want to evaluate an inverse function, we find its input within its domain, which is all or part of the vertical axis of the original function’s graph.
Given the graph of a function, evaluate its inverse at specific points.
A function is given in [link] . Find and
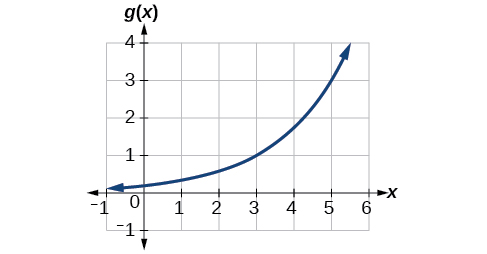
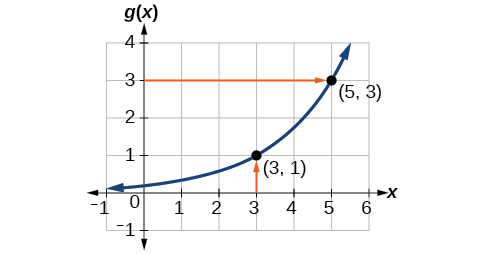
To evaluate we find 3 on the x -axis and find the corresponding output value on the y -axis. The point tells us that
To evaluate recall that by definition means the value of x for which By looking for the output value 3 on the vertical axis, we find the point on the graph, which means so by definition, See [link] .

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?