| << Chapter < Page | Chapter >> Page > |
Identify the degree, leading term, and leading coefficient of the following polynomial functions.
For the function the highest power of is 3, so the degree is 3. The leading term is the term containing that degree, The leading coefficient is the coefficient of that term,
For the function the highest power of is so the degree is The leading term is the term containing that degree, The leading coefficient is the coefficient of that term,
For the function the highest power of is so the degree is The leading term is the term containing that degree, The leading coefficient is the coefficient of that term,
Identify the degree, leading term, and leading coefficient of the polynomial
The degree is 6. The leading term is The leading coefficient is
Knowing the degree of a polynomial function is useful in helping us predict its end behavior. To determine its end behavior, look at the leading term of the polynomial function. Because the power of the leading term is the highest, that term will grow significantly faster than the other terms as gets very large or very small, so its behavior will dominate the graph. For any polynomial, the end behavior of the polynomial will match the end behavior of the power function consisting of the leading term. See [link] .
| Polynomial Function | Leading Term | Graph of Polynomial Function |
|---|---|---|
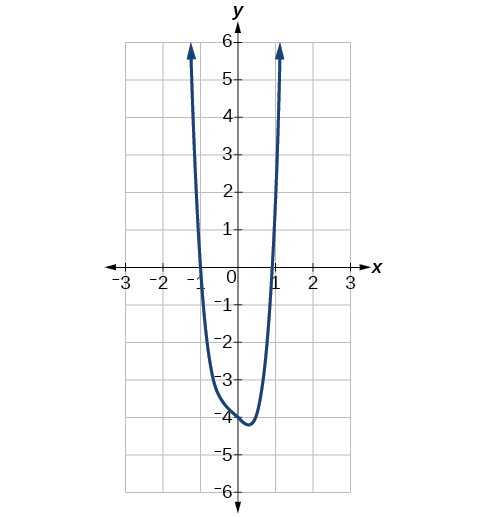 | ||
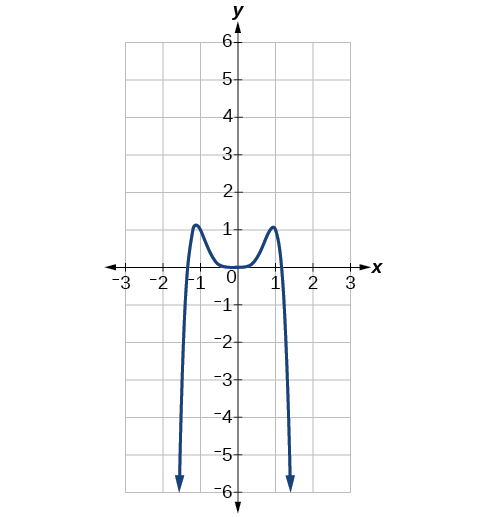 | ||
 | ||
 |
Describe the end behavior and determine a possible degree of the polynomial function in [link] .
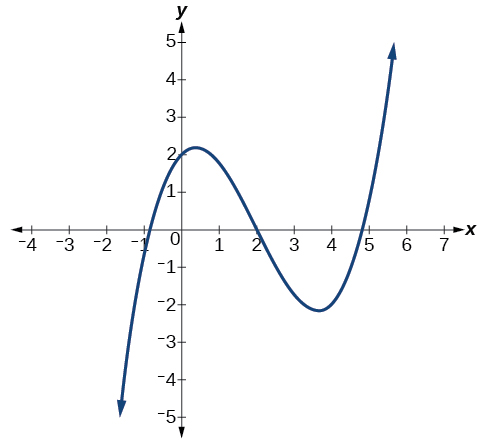
As the input values get very large, the output values increase without bound. As the input values get very small, the output values decrease without bound. We can describe the end behavior symbolically by writing
In words, we could say that as values approach infinity, the function values approach infinity, and as values approach negative infinity, the function values approach negative infinity.
We can tell this graph has the shape of an odd degree power function that has not been reflected, so the degree of the polynomial creating this graph must be odd and the leading coefficient must be positive.
Describe the end behavior, and determine a possible degree of the polynomial function in [link] .

As It has the shape of an even degree power function with a negative coefficient.
Given the function express the function as a polynomial in general form, and determine the leading term, degree, and end behavior of the function.
Obtain the general form by expanding the given expression for
The general form is The leading term is therefore, the degree of the polynomial is 4. The degree is even (4) and the leading coefficient is negative (–3), so the end behavior is

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?