| << Chapter < Page | Chapter >> Page > |

A band marches down the field creating an amazing sound that bolsters the crowd. That sound travels as a wave that can be interpreted using trigonometric functions. For example, [link] represents a sound wave for the musical note A. In this section, we will investigate trigonometric identities that are the foundation of everyday phenomena such as sound waves.
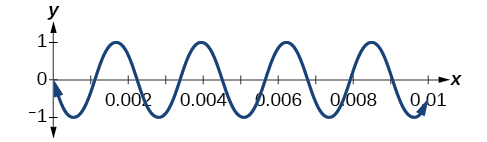
We have already learned a number of formulas useful for expanding or simplifying trigonometric expressions, but sometimes we may need to express the product of cosine and sine as a sum. We can use the product-to-sum formulas , which express products of trigonometric functions as sums. Let’s investigate the cosine identity first and then the sine identity.
We can derive the product-to-sum formula from the sum and difference identities for cosine . If we add the two equations, we get:
Then, we divide by to isolate the product of cosines:
Given a product of cosines, express as a sum.
Write the following product of cosines as a sum:
We begin by writing the formula for the product of cosines:
We can then substitute the given angles into the formula and simplify.
Use the product-to-sum formula to write the product as a sum or difference:
Next, we will derive the product-to-sum formula for sine and cosine from the sum and difference formulas for sine . If we add the sum and difference identities, we get:
Then, we divide by 2 to isolate the product of cosine and sine:
Express the following product as a sum containing only sine or cosine and no products:
Write the formula for the product of sine and cosine. Then substitute the given values into the formula and simplify.
Use the product-to-sum formula to write the product as a sum:
Expressing the product of sines in terms of cosine is also derived from the sum and difference identities for cosine. In this case, we will first subtract the two cosine formulas:

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?