| << Chapter < Page | Chapter >> Page > |
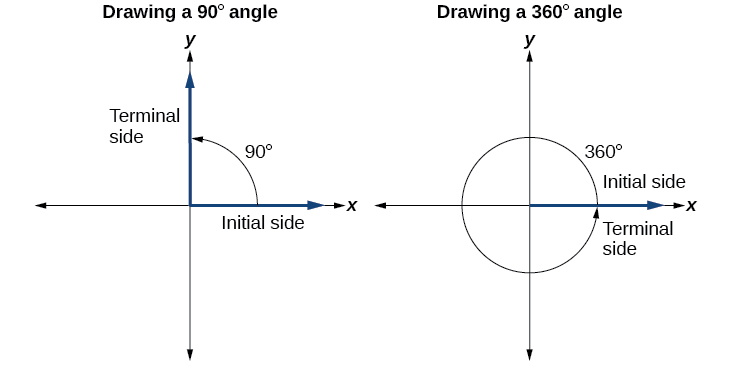
Drawing an angle in standard position always starts the same way—draw the initial side along the positive x -axis. To place the terminal side of the angle, we must calculate the fraction of a full rotation the angle represents. We do that by dividing the angle measure in degrees by For example, to draw a angle, we calculate that So, the terminal side will be one-fourth of the way around the circle, moving counterclockwise from the positive x -axis. To draw a angle, we calculate that So the terminal side will be 1 complete rotation around the circle, moving counterclockwise from the positive x -axis. In this case, the initial side and the terminal side overlap. See [link] .
Since we define an angle in standard position by its terminal side, we have a special type of angle whose terminal side lies on an axis, a quadrantal angle . This type of angle can have a measure of or See [link] .
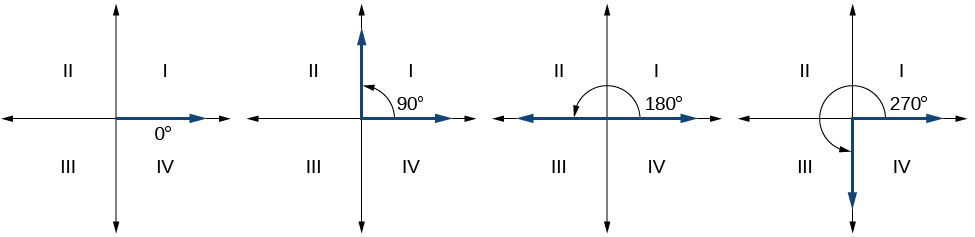
An angle is a quadrantal angle if its terminal side lies on an axis, including or
Given an angle measure in degrees, draw the angle in standard position.
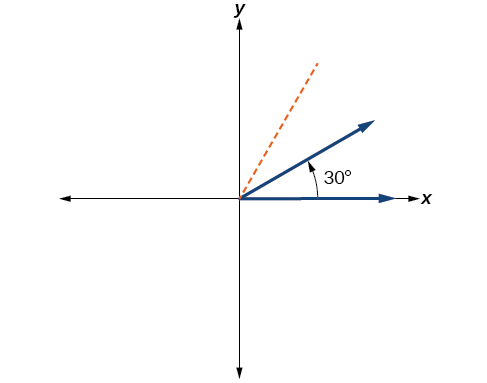
Divide the angle measure by
To rewrite the fraction in a more familiar fraction, we can recognize that
One-twelfth equals one-third of a quarter, so by dividing a quarter rotation into thirds, we can sketch a line at as in [link] .
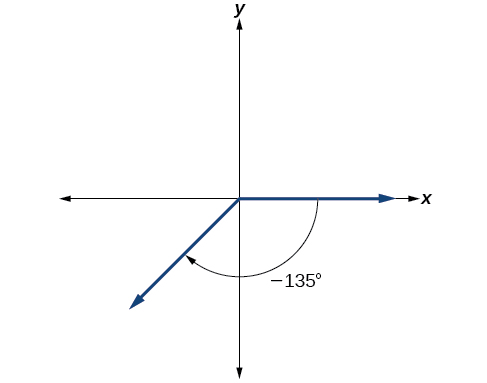
Divide the angle measure by
In this case, we can recognize that
Negative three-eighths is one and one-half times a quarter, so we place a line by moving clockwise one full quarter and one-half of another quarter, as in [link] .
Dividing a circle into 360 parts is an arbitrary choice, although it creates the familiar degree measurement. We may choose other ways to divide a circle. To find another unit, think of the process of drawing a circle. Imagine that you stop before the circle is completed. The portion that you drew is referred to as an arc. An arc may be a portion of a full circle, a full circle, or more than a full circle, represented by more than one full rotation. The length of the arc around an entire circle is called the circumference of that circle.
The circumference of a circle is If we divide both sides of this equation by we create the ratio of the circumference, which is always to the radius, regardless of the length of the radius. So the circumference of any circle is times the length of the radius. That means that if we took a string as long as the radius and used it to measure consecutive lengths around the circumference, there would be room for six full string-lengths and a little more than a quarter of a seventh, as shown in [link] .

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?