| << Chapter < Page | Chapter >> Page > |
A golfer swings to hit a ball over a sand trap and onto the green. An airline pilot maneuvers a plane toward a narrow runway. A dress designer creates the latest fashion. What do they all have in common? They all work with angles, and so do all of us at one time or another. Sometimes we need to measure angles exactly with instruments. Other times we estimate them or judge them by eye. Either way, the proper angle can make the difference between success and failure in many undertakings. In this section, we will examine properties of angles.
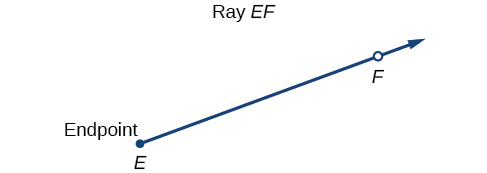
Properly defining an angle first requires that we define a ray. A ray is a directed line segment. It consists of one point on a line and all points extending in one direction from that point. The first point is called the endpoint of the ray. We can refer to a specific ray by stating its endpoint and any other point on it. The ray in [link] can be named as ray EF, or in symbol form
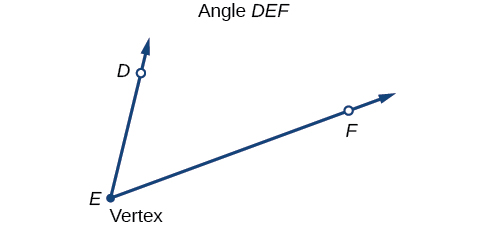
An angle is the union of two rays having a common endpoint. The endpoint is called the vertex of the angle, and the two rays are the sides of the angle. The angle in [link] is formed from and . Angles can be named using a point on each ray and the vertex, such as angle DEF , or in symbol form
Greek letters are often used as variables for the measure of an angle. [link] is a list of Greek letters commonly used to represent angles, and a sample angle is shown in [link] .
| or | ||||
|---|---|---|---|---|
| theta | phi | alpha | beta | gamma |
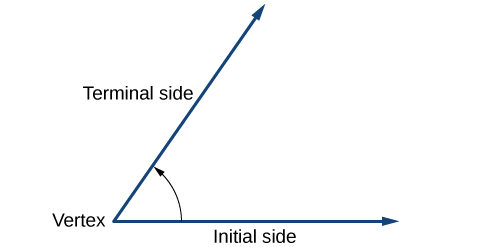
Angle creation is a dynamic process. We start with two rays lying on top of one another. We leave one fixed in place, and rotate the other. The fixed ray is the initial side , and the rotated ray is the terminal side . In order to identify the different sides, we indicate the rotation with a small arrow close to the vertex as in [link] .
As we discussed at the beginning of the section, there are many applications for angles, but in order to use them correctly, we must be able to measure them. The measure of an angle is the amount of rotation from the initial side to the terminal side. Probably the most familiar unit of angle measurement is the degree. One degree is of a circular rotation, so a complete circular rotation contains degrees. An angle measured in degrees should always include the unit “degrees” after the number, or include the degree symbol For example,
To formalize our work, we will begin by drawing angles on an x - y coordinate plane. Angles can occur in any position on the coordinate plane, but for the purpose of comparison, the convention is to illustrate them in the same position whenever possible. An angle is in standard position if its vertex is located at the origin, and its initial side extends along the positive x -axis. See [link] .
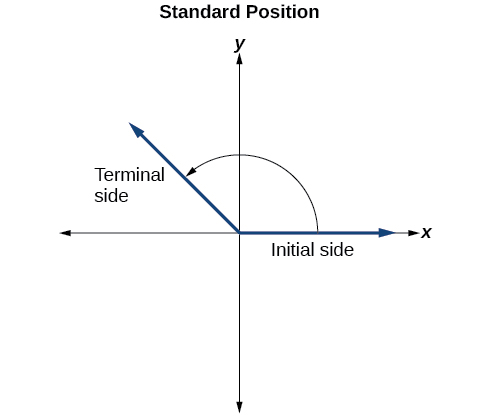
If the angle is measured in a counterclockwise direction from the initial side to the terminal side, the angle is said to be a positive angle . If the angle is measured in a clockwise direction, the angle is said to be a negative angle .

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?