| << Chapter < Page | Chapter >> Page > |
Write the formula for the function that we get when we stretch the identity toolkit function by a factor of 3, and then shift it down by 2 units.
Now we consider changes to the inside of a function. When we multiply a function’s input by a positive constant, we get a function whose graph is stretched or compressed horizontally in relation to the graph of the original function. If the constant is between 0 and 1, we get a horizontal stretch ; if the constant is greater than 1, we get a horizontal compression of the function.
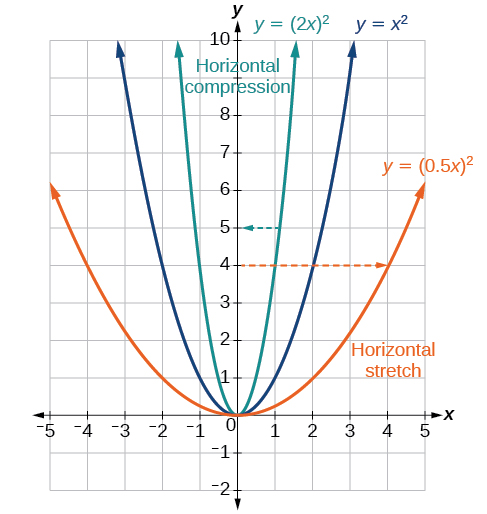
Given a function the form results in a horizontal stretch or compression. Consider the function Observe [link] . The graph of is a horizontal stretch of the graph of the function by a factor of 2. The graph of is a horizontal compression of the graph of the function by a factor of 2.
Given a function a new function where is a constant, is a horizontal stretch or horizontal compression of the function
Given a description of a function, sketch a horizontal compression or stretch.
Suppose a scientist is comparing a population of fruit flies to a population that progresses through its lifespan twice as fast as the original population. In other words, this new population, will progress in 1 hour the same amount as the original population does in 2 hours, and in 2 hours, it will progress as much as the original population does in 4 hours. Sketch a graph of this population.
Symbolically, we could write
See [link] for a graphical comparison of the original population and the compressed population.
![Two side-by-side graphs. The first graph has function for original population whose domain is [0,7] and range is [0,3]. The maximum value occurs at (3,3). The second graph has the same shape as the first except it is half as wide. It is a graph of transformed population, with a domain of [0, 3.5] and a range of [0,3]. The maximum occurs at (1.5, 3).](/ocw/mirror/col11758/m51266/CNX_Precalc_Figure_01_05_029ab.jpg)
A function is given as [link] . Create a table for the function
| 2 | 4 | 6 | 8 | |
| 1 | 3 | 7 | 11 |
The formula tells us that the output values for are the same as the output values for the function at an input half the size. Notice that we do not have enough information to determine because and we do not have a value for in our table. Our input values to will need to be twice as large to get inputs for that we can evaluate. For example, we can determine
We do the same for the other values to produce [link] .
| 4 | 8 | 12 | 16 | |
| 1 | 3 | 7 | 11 |
[link] shows the graphs of both of these sets of points.
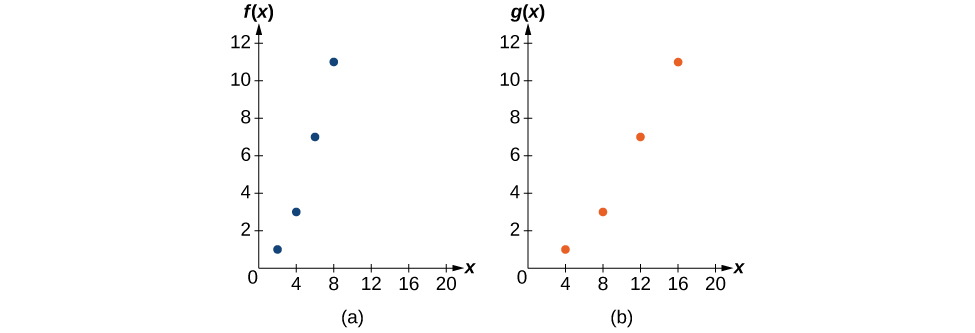
The graph of looks like the graph of horizontally compressed. Because ends at and ends at we can see that the values have been compressed by because We might also notice that and Either way, we can describe this relationship as This is a horizontal compression by

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?