| << Chapter < Page | Chapter >> Page > |
Given a tabular function, create a new row to represent a horizontal shift.
A function is given in [link] . Create a table for the function
| 2 | 4 | 6 | 8 | |
| 1 | 3 | 7 | 11 |
The formula tells us that the output values of are the same as the output value of when the input value is 3 less than the original value. For example, we know that To get the same output from the function we will need an input value that is 3 larger . We input a value that is 3 larger for because the function takes 3 away before evaluating the function
We continue with the other values to create [link] .
| 5 | 7 | 9 | 11 | |
| 2 | 4 | 6 | 8 | |
| 1 | 3 | 7 | 11 | |
| 1 | 3 | 7 | 11 |
The result is that the function has been shifted to the right by 3. Notice the output values for remain the same as the output values for but the corresponding input values, have shifted to the right by 3. Specifically, 2 shifted to 5, 4 shifted to 7, 6 shifted to 9, and 8 shifted to 11.
[link] represents a transformation of the toolkit function Relate this new function to and then find a formula for
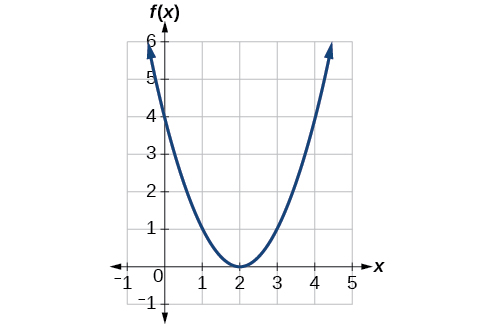
Notice that the graph is identical in shape to the function, but the x- values are shifted to the right 2 units. The vertex used to be at (0,0), but now the vertex is at (2,0). The graph is the basic quadratic function shifted 2 units to the right, so
Notice how we must input the value to get the output value the x -values must be 2 units larger because of the shift to the right by 2 units. We can then use the definition of the function to write a formula for by evaluating
The function gives the number of gallons of gas required to drive miles. Interpret and
can be interpreted as adding 10 to the output, gallons. This is the gas required to drive miles, plus another 10 gallons of gas. The graph would indicate a vertical shift.
can be interpreted as adding 10 to the input, miles. So this is the number of gallons of gas required to drive 10 miles more than miles. The graph would indicate a horizontal shift.
Given the function graph the original function and the transformation on the same axes. Is this a horizontal or a vertical shift? Which way is the graph shifted and by how many units?
The graphs of and are shown below. The transformation is a horizontal shift. The function is shifted to the left by 2 units.

Now that we have two transformations, we can combine them. Vertical shifts are outside changes that affect the output ( y -) values and shift the function up or down. Horizontal shifts are inside changes that affect the input ( x -) values and shift the function left or right. Combining the two types of shifts will cause the graph of a function to shift up or down and left or right.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?