| << Chapter < Page | Chapter >> Page > |
For the following exercises, draw an angle in standard position with the given measure.
For the following exercises, refer to [link] . Round to two decimal places.
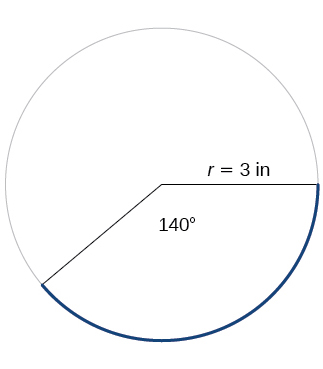
Find the arc length.
For the following exercises, refer to [link] . Round to two decimal places.
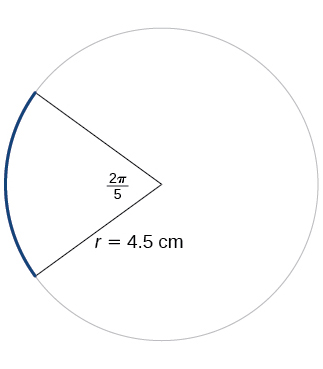
Find the arc length.
For the following exercises, convert angles in radians to degrees.
For the following exercises, convert angles in degrees to radians.
For the following exercises, use the given information to find the length of a circular arc. Round to two decimal places.
Find the length of the arc of a circle of radius 12 inches subtended by a central angle of radians.
Find the length of the arc of a circle of radius 5.02 miles subtended by the central angle of
miles
Find the length of the arc of a circle of diameter 14 meters subtended by the central angle of
Find the length of the arc of a circle of radius 10 centimeters subtended by the central angle of
centimeters
Find the length of the arc of a circle of radius 5 inches subtended by the central angle of
Find the length of the arc of a circle of diameter 12 meters subtended by the central angle is
meters
For the following exercises, use the given information to find the area of the sector. Round to four decimal places.
A sector of a circle has a central angle of and a radius 6 cm.
A sector of a circle has a central angle of and a radius of 20 cm.
104.7198 cm 2
A sector of a circle with diameter 10 feet and an angle of radians.
A sector of a circle with radius of 0.7 inches and an angle of radians.
0.7697 in 2
For the following exercises, find the angle between and that is coterminal to the given angle.
For the following exercises, find the angle between 0 and in radians that is coterminal to the given angle.
A truck with 32-inch diameter wheels is traveling at 60 mi/h. Find the angular speed of the wheels in rad/min. How many revolutions per minute do the wheels make?
A bicycle with 24-inch diameter wheels is traveling at 15 mi/h. Find the angular speed of the wheels in rad/min. How many revolutions per minute do the wheels make?
rad/min RPM
A wheel of radius 8 inches is rotating 15°/s. What is the linear speed the angular speed in RPM, and the angular speed in rad/s?
A wheel of radius inches is rotating rad/s. What is the linear speed the angular speed in RPM, and the angular speed in deg/s?
in./s, 4.77 RPM , deg/s
A CD has diameter of 120 millimeters. When playing audio, the angular speed varies to keep the linear speed constant where the disc is being read. When reading along the outer edge of the disc, the angular speed is about 200 RPM (revolutions per minute). Find the linear speed.
When being burned in a writable CD-R drive, the angular speed of a CD is often much faster than when playing audio, but the angular speed still varies to keep the linear speed constant where the disc is being written. When writing along the outer edge of the disc, the angular speed of one drive is about 4800 RPM (revolutions per minute). Find the linear speed if the CD has diameter of 120 millimeters.
A person is standing on the equator of Earth (radius 3960 miles). What are his linear and angular speeds?
Find the distance along an arc on the surface of Earth that subtends a central angle of 5 minutes
. The radius of Earth is 3960 miles.
miles
Find the distance along an arc on the surface of Earth that subtends a central angle of 7 minutes
. The radius of Earth is
miles.
Consider a clock with an hour hand and minute hand. What is the measure of the angle the minute hand traces in minutes?
Two cities have the same longitude. The latitude of city A is 9.00 degrees north and the latitude of city B is 30.00 degree north. Assume the radius of the earth is 3960 miles. Find the distance between the two cities.
A city is located at 40 degrees north latitude. Assume the radius of the earth is 3960 miles and the earth rotates once every 24 hours. Find the linear speed of a person who resides in this city.
794 miles per hour
A city is located at 75 degrees north latitude. Assume the radius of the earth is 3960 miles and the earth rotates once every 24 hours. Find the linear speed of a person who resides in this city.
Find the linear speed of the moon if the average distance between the earth and moon is 239,000 miles, assuming the orbit of the moon is circular and requires about 28 days. Express answer in miles per hour.
2,234 miles per hour
A bicycle has wheels 28 inches in diameter. A tachometer determines that the wheels are rotating at 180 RPM (revolutions per minute). Find the speed the bicycle is travelling down the road.
A car travels 3 miles. Its tires make 2640 revolutions. What is the radius of a tire in inches?
11.5 inches
A wheel on a tractor has a 24-inch diameter. How many revolutions does the wheel make if the tractor travels 4 miles?
3361 revolutions

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?