| << Chapter < Page | Chapter >> Page > |
If is a real number and a point on the unit circle corresponds to a central angle then
Given a point P on the unit circle corresponding to an angle of find the sine and cosine.
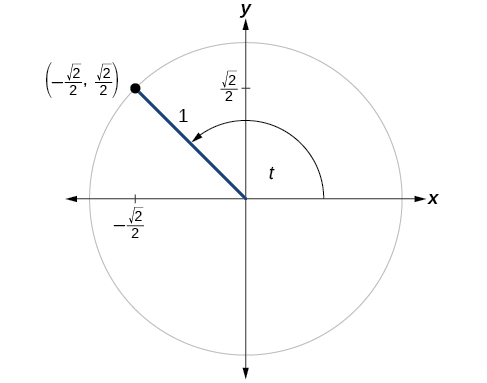
Point is a point on the unit circle corresponding to an angle of as shown in [link] . Find and

We know that is the x -coordinate of the corresponding point on the unit circle and is the y -coordinate of the corresponding point on the unit circle. So:
A certain angle corresponds to a point on the unit circle at as shown in [link] . Find and
For quadrantral angles, the corresponding point on the unit circle falls on the x- or y -axis. In that case, we can easily calculate cosine and sine from the values of and
Find and
Moving counterclockwise around the unit circle from the positive x -axis brings us to the top of the circle, where the coordinates are as shown in [link] .
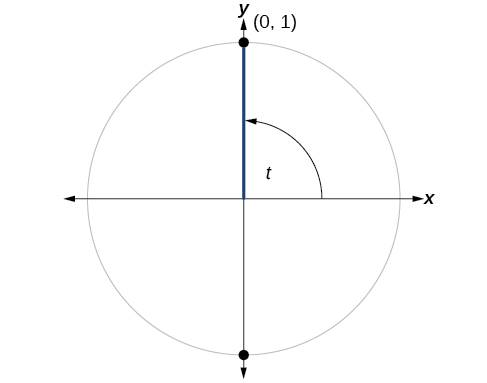
We can then use our definitions of cosine and sine.
The cosine of is 0; the sine of is 1.
Now that we can define sine and cosine, we will learn how they relate to each other and the unit circle. Recall that the equation for the unit circle is Because and we can substitute for and to get This equation, is known as the Pythagorean Identity . See [link] .
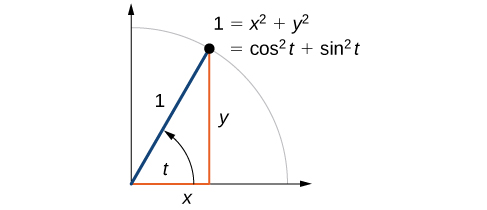
We can use the Pythagorean Identity to find the cosine of an angle if we know the sine, or vice versa. However, because the equation yields two solutions, we need additional knowledge of the angle to choose the solution with the correct sign. If we know the quadrant where the angle is, we can easily choose the correct solution.
The Pythagorean Identity states that, for any real number
Given the sine of some angle and its quadrant location, find the cosine of
If and is in the second quadrant, find
If we drop a vertical line from the point on the unit circle corresponding to we create a right triangle, from which we can see that the Pythagorean Identity is simply one case of the Pythagorean Theorem. See [link] .
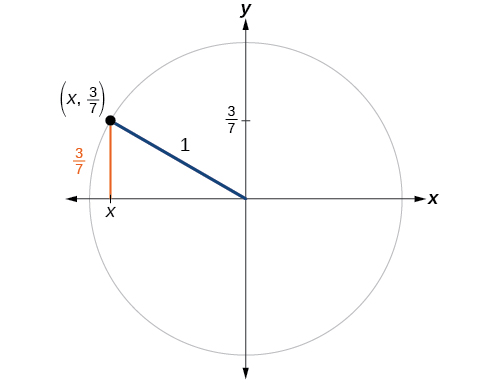
Substituting the known value for sine into the Pythagorean Identity,
Because the angle is in the second quadrant, we know the x- value is a negative real number, so the cosine is also negative.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?