| << Chapter < Page | Chapter >> Page > |
We have already learned some properties of the special angles, such as the conversion from radians to degrees, and we found their sines and cosines using right triangles. We can also calculate sines and cosines of the special angles using the Pythagorean Identity.
First, we will look at angles of or as shown in [link] . A triangle is an isosceles triangle, so the x- and y -coordinates of the corresponding point on the circle are the same. Because the x- and y -values are the same, the sine and cosine values will also be equal.
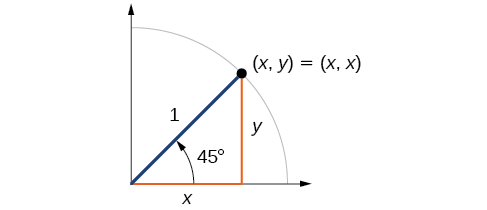
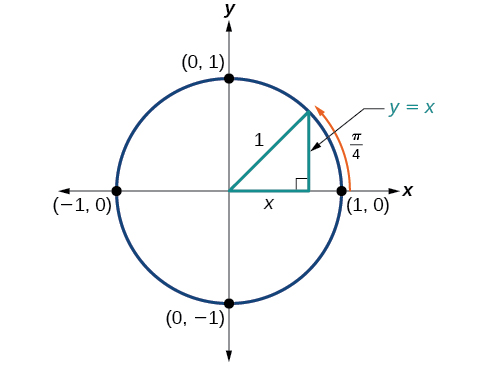
At which is 45 degrees, the radius of the unit circle bisects the first quadrantal angle. This means the radius lies along the line A unit circle has a radius equal to 1 so the right triangle formed below the line has sides and and radius = 1. See [link] .
From the Pythagorean Theorem we get
We can then substitute
Next we combine like terms.
And solving for we get
In quadrant I,
At or 45 degrees,
If we then rationalize the denominators, we get
Therefore, the coordinates of a point on a circle of radius at an angle of are
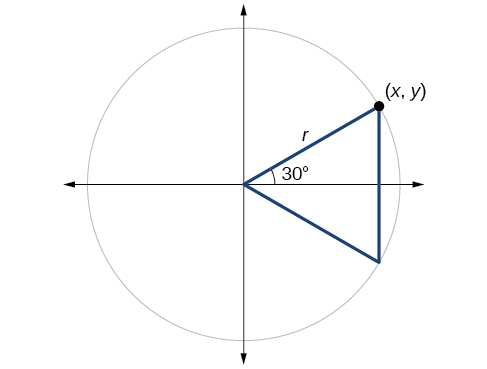
Next, we will find the cosine and sine at an angle of or First, we will draw a triangle inside a circle with one side at an angle of and another at an angle of as shown in [link] . If the resulting two right triangles are combined into one large triangle, notice that all three angles of this larger triangle will be as shown in [link] .
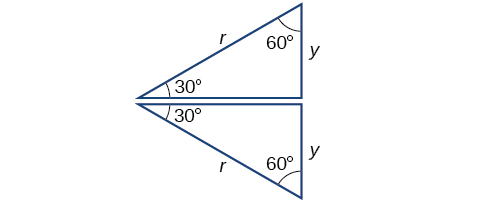
Because all the angles are equal, the sides are also equal. The vertical line has length and since the sides are all equal, we can also conclude that or Since
And since in our unit circle,
Using the Pythagorean Identity, we can find the cosine value.
The coordinates for the point on a circle of radius at an angle of are At the radius of the unit circle, 1, serves as the hypotenuse of a 30-60-90 degree right triangle, as shown in [link] . Angle has measure At point we draw an angle with measure of We know the angles in a triangle sum to so the measure of angle is also Now we have an equilateral triangle. Because each side of the equilateral triangle is the same length, and we know one side is the radius of the unit circle, all sides must be of length 1.
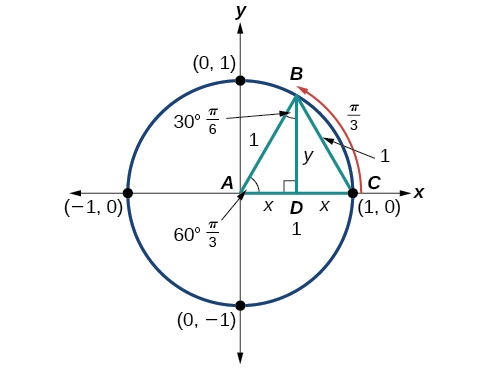
The measure of angle is 30°. Angle is double angle so its measure is 60°. is the perpendicular bisector of so it cuts in half. This means that is the radius, or Notice that is the x -coordinate of point which is at the intersection of the 60° angle and the unit circle. This gives us a triangle with hypotenuse of 1 and side of length

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?