| << Chapter < Page | Chapter >> Page > |
A professor is attempting to identify trends among final exam scores. His class has a mixture of students, so he wonders if there is any relationship between age and final exam scores. One way for him to analyze the scores is by creating a diagram that relates the age of each student to the exam score received. In this section, we will examine one such diagram known as a scatter plot.
A scatter plot is a graph of plotted points that may show a relationship between two sets of data. If the relationship is from a linear model , or a model that is nearly linear, the professor can draw conclusions using his knowledge of linear functions. [link] shows a sample scatter plot.
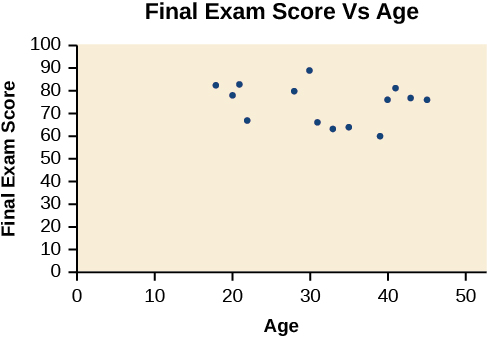
Notice this scatter plot does not indicate a linear relationship . The points do not appear to follow a trend. In other words, there does not appear to be a relationship between the age of the student and the score on the final exam.
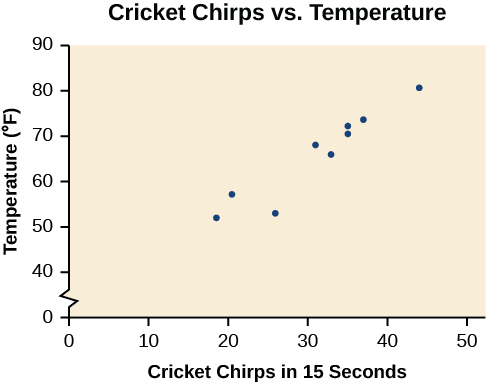
[link] shows the number of cricket chirps in 15 seconds, for several different air temperatures, in degrees Fahrenheit Selected data from http://classic.globe.gov/fsl/scientistsblog/2007/10/. Retrieved Aug 3, 2010 . Plot this data, and determine whether the data appears to be linearly related.
| Chirps | 44 | 35 | 20.4 | 33 | 31 | 35 | 18.5 | 37 | 26 |
| Temperature | 80.5 | 70.5 | 57 | 66 | 68 | 72 | 52 | 73.5 | 53 |
Plotting this data, as depicted in [link] suggests that there may be a trend. We can see from the trend in the data that the number of chirps increases as the temperature increases. The trend appears to be roughly linear, though certainly not perfectly so.
Once we recognize a need for a linear function to model that data, the natural follow-up question is “what is that linear function?” One way to approximate our linear function is to sketch the line that seems to best fit the data. Then we can extend the line until we can verify the y -intercept. We can approximate the slope of the line by extending it until we can estimate the
Find a linear function that fits the data in [link] by “eyeballing” a line that seems to fit.
On a graph, we could try sketching a line. Using the starting and ending points of our hand drawn line, points (0, 30) and (50, 90), this graph has a slope of
and a y -intercept at 30. This gives an equation of
where is the number of chirps in 15 seconds, and is the temperature in degrees Fahrenheit. The resulting equation is represented in [link] .
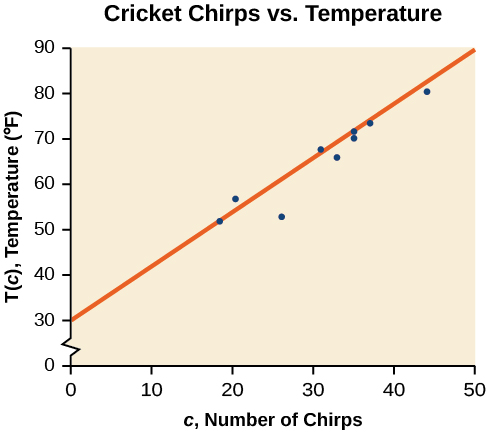
While the data for most examples does not fall perfectly on the line, the equation is our best guess as to how the relationship will behave outside of the values for which we have data. We use a process known as interpolation when we predict a value inside the domain and range of the data. The process of extrapolation is used when we predict a value outside the domain and range of the data.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?