| << Chapter < Page | Chapter >> Page > |
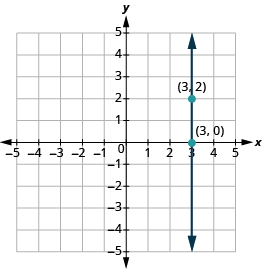
| What is the rise? | The rise is 2. |
| What is the run? | The run is 0. |
| What is the slope? | |
But we can’t divide by Division by is undefined. So we say that the slope of the vertical line is undefined. The slope of all vertical lines is undefined, because the run is
The slope of a vertical line , is undefined.
Find the slope of each line:
ⓐ
This is a vertical line, so its slope is undefined.
ⓑ
This is a horizontal line, so its slope is
Sometimes we need to find the slope of a line between two points and we might not have a graph to count out the rise and the run. We could plot the points on grid paper, then count out the rise and the run, but there is a way to find the slope without graphing.
Before we get to it, we need to introduce some new algebraic notation. We have seen that an ordered pair gives the coordinates of a point. But when we work with slopes, we use two points. How can the same symbol be used to represent two different points?
Mathematicians use subscripts to distinguish between the points. A subscript is a small number written to the right of, and a little lower than, a variable.
We will use to identify the first point and to identify the second point. If we had more than two points, we could use and so on.
To see how the rise and run relate to the coordinates of the two points, let’s take another look at the slope of the line between the points and in [link] .
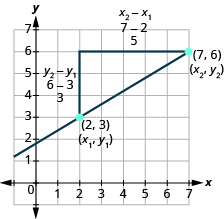
Since we have two points, we will use subscript notation.
On the graph, we counted the rise of The rise can also be found by subtracting the of the points.
We counted a run of The run can also be found by subtracting the
| We know | |
| So | |
| We rewrite the rise and run by putting in the coordinates. | |
| But 6 is the
-coordinate of the second point,
and 3 is the -coordinate of the first point . So we can rewrite the rise using subscript notation. |
|
| Also 7 is the
-coordinate of the second point,
and 2 is the -coordinate of the first point . So we rewrite the run using subscript notation. |
We’ve shown that is really another version of We can use this formula to find the slope of a line when we have two points on the line.
The slope of the line between two points and is
Say the formula to yourself to help you remember it:
Find the slope of the line between the points and
| We’ll call point #1 and point #2. | |
| Use the slope formula. | |
| Substitute the values in the slope formula: | |
| of the second point minus of the first point | |
| of the second point minus of the first point | |
| Simplify the numerator and the denominator. | |
Let’s confirm this by counting out the slope on the graph.
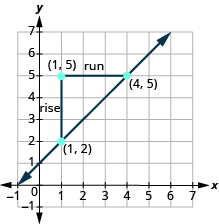
The rise is and the run is so

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?