| << Chapter < Page | Chapter >> Page > |
The key is to understand that a standing wave must be created in the medium that is oscillating. There are restrictions as to whatwavelengths can form standing waves in a medium.
For example, if we consider a rope that can move in a pipe such that it can have
Each of these cases is slightly different because the free or fixed end determines whether a node or anti-node will form when a standingwave is created in the rope. These are the main restrictions when we determine the wavelengths of potential standing waves. These restrictions are known as boundary conditions and must be met.
In the diagram below you can see the three different cases. It is possible to create standing waves with different frequencies andwavelengths as long as the end criteria are met.

The longer the wavelength the less the number of anti-nodes in the standing waves. We cannot have a standing wave with no anti-nodes becausethen there would be no oscillations. We use to number the anti-nodes. If all of the tubes have a length and we know the end constraints we can find the wavelength, , for a specific number of anti-nodes.
Let's work out the longest wavelength we can have in each tube, i.e. the case for .

Case 1 : In the first tube, both ends must be anti-nodes, so we must place onenode in the middle of the tube. We know the distance from one anti-node to another is and we also know this distance is L. So we can equate the two and solve for the wavelength:
Case 2 : In the second tube, one end must be a node and the other must be ananti-node. Since we are looking at the case with one node, we are forced to have it at the end. We know the distance from onenode to another is but we only have half this distance contained in the tube. So :
Case 3 : Here both ends are closed and so we must have two nodes so it isimpossible to construct a case with only one node.
Next we determine which wavelengths could be formed if we had two nodes. Remember that we are dividing the tube up into smaller andsmaller segments by having more nodes so we expect the wavelengths to get shorter.
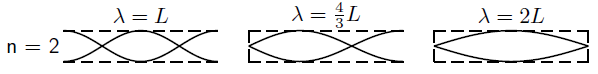
Case 1 : Both ends are open and so they must be anti-nodes. We can have twonodes inside the tube only if we have one anti-node contained inside the tube and one on each end. This means we have 3 anti-nodes in thetube. The distance between any two anti-nodes is half a wavelength. This means there is half wavelength between the left sideand the middle and another half wavelength between the middle and the right side so there must be one wavelength inside the tube. The safestthing to do is work out how many half wavelengths there are and equatethis to the length of the tube L and then solve for .
Case 2 : We want to have two nodes inside the tube. The left end must be anode and the right end must be an anti-node. We can have one node inside the tube as drawn above. Again we can count the number ofdistances between adjacent nodes or anti-nodes. If we start from the left end we have one half wavelength between the end and the nodeinside the tube. The distance from the node inside the tube to the right end which is an anti-node is half of the distance to anothernode. So it is half of half a wavelength. Together these add up to the length of the tube:

Notification Switch
Would you like to follow the 'Physics - grade 10 [caps 2011]' conversation and receive update notifications?