Solve
for
Got questions? Get instant answers now!
Practice set b
Solve and check each equation.
Often the variable we wish to solve for will appear on both sides of the equal sign. We can isolate the variable on either the left or right side of the equation by using the techniques of Sections
[link] and
[link] .
Sample set c
Solve
for
Got questions? Get instant answers now!
Solve
for
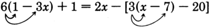
Got questions? Get instant answers now!
Practice set c
Recognizing identities and contradictions
As we noted in Section
[link] , some equations are identities and some are contradictions. As the problems of Sample Set D will suggest,
Recognizing an identity
- If, when solving an equation, all the variables are eliminated and a true statement results, the equation is an
identity.
Recognizing a contradiction
- If, when solving an equation, all the variables are eliminated and a false statement results, the equation is a
contradiction.
Sample set d
Solve
for
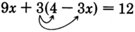
The variable has been eliminated and the result is a true statement. The original equation is an
identity.
Got questions? Get instant answers now!
Solve
for
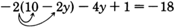
The variable has been eliminated and the result is a false statement. The original equation is a
contradiction.
Got questions? Get instant answers now!
Practice set d
Classify each equation as an identity or a contradiction.
Exercises
For the following problems, solve each conditional equation. If the equation is not conditional, identify it as an identity or a contradiction.
For the following problems, solve the literal equations for the indicated variable. When directed, find the value of that variable for the given values of the other variables.
Solve
for
represents a single quantity. Find the value of
when
and
Got questions? Get instant answers now!
Exercises for review
![]()
![]()
![]() for
for
![]() .
.