| << Chapter < Page | Chapter >> Page > |
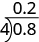
Notice that the decimal point in the quotient is directly above the decimal point in the dividend.
To divide a decimal by a whole number, we place the decimal point in the quotient above the decimal point in the dividend and then divide as usual. Sometimes we need to use extra zeros at the end of the dividend to keep dividing until there is no remainder.
Divide:
| Write as long division, placing the decimal point in the quotient above the decimal point in the dividend. |
|
| Divide as usual. Since 3 does not go into 0 or 1 we use zeros as placeholders. |
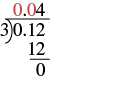 |
In everyday life, we divide whole numbers into decimals—money—to find the price of one item. For example, suppose a case of water bottles cost To find the price per water bottle, we would divide by and round the answer to the nearest cent (hundredth).
Divide:
| Place the decimal point in the quotient above the decimal point in the dividend. |
|
| Divide as usual. When do we stop? Since this division involves money, we round it to the nearest cent (hundredth). To do this, we must carry the division to the thousandths place. |
 |
| Round to the nearest cent. | |
This means the price per bottle is cents.
So far, we have divided a decimal by a whole number. What happens when we divide a decimal by another decimal? Let’s look at the same multiplication problem we looked at earlier, but in a different way.
Remember, again, that a multiplication problem can be rephrased as a division problem. This time we ask, “How many times does go into Because we can say that goes into four times. This means that divided by is

We would get the same answer, if we divide by both whole numbers. Why is this so? Let’s think about the division problem as a fraction.
We multiplied the numerator and denominator by and ended up just dividing by To divide decimals, we multiply both the numerator and denominator by the same power of to make the denominator a whole number. Because of the Equivalent Fractions Property, we haven’t changed the value of the fraction. The effect is to move the decimal points in the numerator and denominator the same number of places to the right.
We use the rules for dividing positive and negative numbers with decimals, too. When dividing signed decimals, first determine the sign of the quotient and then divide as if the numbers were both positive. Finally, write the quotient with the appropriate sign.
It may help to review the vocabulary for division:
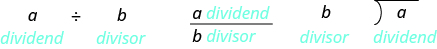

Notification Switch
Would you like to follow the 'Prealgebra' conversation and receive update notifications?