5.4 Triple integrals (Page 4/8)

Calculus volume 3 Page 4 / 8

Changing the order of integration

As we have already seen in double integrals over general bounded regions, changing the order of the integration is done quite often to simplify the computation. With a triple integral over a rectangular box, the order of integration does not change the level of difficulty of the calculation. However, with a triple integral over a general bounded region, choosing an appropriate order of integration can simplify the computation quite a bit. Sometimes making the change to polar coordinates can also be very helpful. We demonstrate two examples here.

Changing the order of integration

Consider the iterated integral

\int_{x = 0}^{x = 1} \int_{y = 0}^{y = x^{2}} \int_{z = 0}^{z = y^{}} f (x, y, z) d z d y d x .

The order of integration here is first with respect to z , then y , and then x . Express this integral by changing the order of integration to be first with respect to x , then z , and then $y .$ Verify that the value of the integral is the same if we let $f (x, y, z) = x y z .$

The best way to do this is to sketch the region $E$ and its projections onto each of the three coordinate planes. Thus, let

E = {(x, y, z) | 0 \leq x \leq 1, 0 \leq y \leq x^{2}, 0 \leq z \leq y} .

and

\int_{x = 0}^{x = 1} \int_{y = 0}^{y = x^{2}} \int_{z = 0}^{z = y^{2}} f (x, y, z) d z d y d x = \underset{E}{∭} f (x, y, z) d V .

We need to express this triple integral as

\int_{y = c}^{y = d} \int_{z = v_{1} (y)}^{z = v_{2} (y)} \int_{x = u_{1} (y, z)}^{x = u_{2} (y, z)} f (x, y, z) d x d z d y .

Knowing the region $E$ we can draw the following projections ( [link] ):

on the $x y$ -plane is $D_{1} = {(x, y) | 0 \leq x \leq 1, 0 \leq y \leq x^{2}} = {(x, y) | 0 \leq y \leq 1, \sqrt{y} \leq x \leq 1},$

on the $y z$ -plane is $D_{2} = {(y, z) | 0 \leq y \leq 1, 0 \leq z \leq y^{2}},$ and

on the $x z$ -plane is $D_{3} = {(x, z) | 0 \leq x \leq 1, 0 \leq z \leq x^{2}} .$

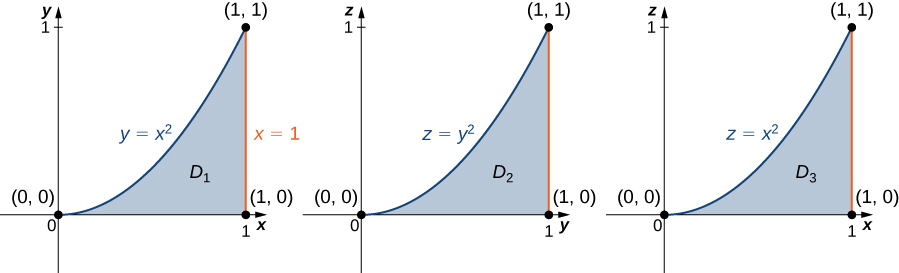
Three similar versions of the following graph are shown: In the x y plane, a region D1 is bounded by the x axis, the line x = 1, and the curve y = x squared. In the second version, region D2 on the z y plane is shown with equation z = y squared. And in the third version, region D3 on the x z plane is shown with equation z = x squared. — The three cross sections of $E$ on the three coordinate planes.

Now we can describe the same region $E$ as ${(x, y, z) | 0 \leq y \leq 1, 0 \leq z \leq y^{2}, \sqrt{y} \leq x \leq 1},$ and consequently, the triple integral becomes

\int_{y = c}^{y = d} \int_{z = v_{1} (y)}^{z = v_{2} (y)} \int_{x = u_{1} (y, z)}^{x = u_{2} (y, z)} f (x, y, z) d x d z d y = \int_{y = 0}^{y = 1} \int_{z = 0}^{z = x^{2}} \int_{x = \sqrt{y}}^{x = 1} f (x, y, z) d x d z d y .

Now assume that $f (x, y, z) = x y z$ in each of the integrals. Then we have

\begin{matrix} \int_{x = 0}^{x = 1} \int_{y = 0}^{y = x^{2}} \int_{z = 0}^{z = y^{2}} x y z d z d y d x \\ = \int_{x = 0}^{x = 1} \int_{y = 0}^{y = x^{2}} [{x y \frac{z^{2}}{2} |}_{z = 0}^{z = y^{2}}] d y d x = \int_{x = 0}^{x = 1} \int_{y = 0}^{y = x^{2}} (x \frac{y^{5}}{2}) d y d x = \int_{x = 0}^{x = 1} [{x \frac{y^{6}}{12} |}_{y = 0}^{y = x^{2}}] d x = \int_{x = 0}^{x = 1} \frac{x^{13}}{12} d x = \frac{1}{168}, \\ \int_{y = 0}^{y = 1} \int_{z = 0}^{z = y^{2}} \int_{x = \sqrt{y}}^{x = 1} x y z d x d z d y \\ = \int_{y = 0}^{y = 1} \int_{z = 0}^{z = y^{2}} [{y z \frac{x^{2}}{2} |}_{\sqrt{y}}^{1}] d z d y \\ = \int_{y = 0}^{y = 1} \int_{z = 0}^{z = y^{2}} (\frac{y z}{2} - \frac{y^{2} z}{2}) d z d y = \int_{y = 0}^{y = 1} [{\frac{y z^{2}}{4} - \frac{y^{2} z^{2}}{4} |}_{z = 0}^{z = y^{2}}] d y = \int_{y = 0}^{y = 1} (\frac{y^{5}}{4} - \frac{y^{6}}{4}) d y = \frac{1}{168} . \end{matrix}

The answers match.

Got questions? Get instant answers now!

Write five different iterated integrals equal to the given integral

\int_{z = 0}^{z = 4} \int_{y = 0}^{y = 4 - z} \int_{x = 0}^{x = \sqrt{y}} f (x, y, z) d x d y d z .

(i) $\int_{z = 0}^{z = 4} \int_{x = 0}^{x = \sqrt{4 - z}} \int_{y = x^{2}}^{y = 4 - z} f (x, y, z) d y d x d z,$ (ii) $\int_{y = 0}^{y = 4} \int_{z = 0}^{z = 4 - y} \int_{x = 0}^{x = \sqrt{y}} f (x, y, z) d x d z d y,$ (iii) $\int_{y = 0}^{y = 4} \int_{x = 0}^{x = \sqrt{y}} \int_{z = 0}^{z = 4 - y} f (x, y, z) d z d x d y,$ (iv) $\int_{x = 0}^{x = 2} \int_{y = x^{2}}^{y = 4} \int_{z = 0}^{z = 4 - y} f (x, y, z) d z d y d x,$ (v) $\int_{x = 0}^{x = 2} \int_{z = 0}^{z = 4 - x^{2}} \int_{y = x^{2}}^{y = 4 - z} f (x, y, z) d y d z d x$

Got questions? Get instant answers now!

Changing integration order and coordinate systems

Evaluate the triple integral $\underset{E}{∭} \sqrt{x^{2} + z^{2}} d V,$ where $E$ is the region bounded by the paraboloid $y = x^{2} + z^{2}$ ( [link] ) and the plane $y = 4 .$

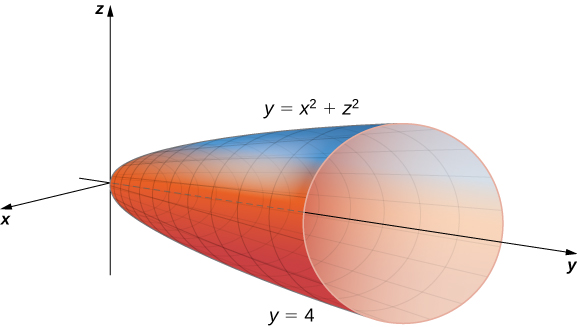
The paraboloid y = x squared + z squared is shown opening up along the y axis to y = 4. — Integrating a triple integral over a paraboloid.

The projection of the solid region $E$ onto the $x y$ -plane is the region bounded above by $y = 4$ and below by the parabola $y = x^{2}$ as shown.

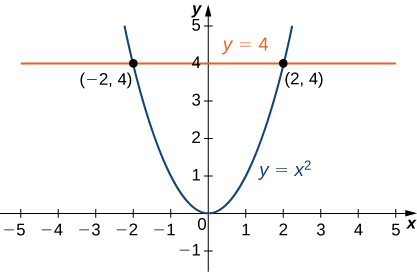
In the x y plane, the graph of y = x squared is shown with the line y = 4 intersecting the graph at (negative 2, 4) and (2, 4). — Cross section in the $x y$ -plane of the paraboloid in [link] .

Thus, we have

E = {(x, y, z) | - 2 \leq x \leq 2, x^{2} \leq y \leq 4, − \sqrt{y - x^{2}} \leq z \leq \sqrt{y - x^{2}}} .

The triple integral becomes

\underset{E}{∭} \sqrt{x^{2} + z^{2}} d V = \int_{x = −2}^{x = 2} \int_{y = x^{2}}^{y = 4} \int_{z = − \sqrt{y - x^{2}}}^{z = \sqrt{y - x^{2}}} \sqrt{x^{2} + z^{2}} d z d y d x .

This expression is difficult to compute, so consider the projection of $E$ onto the $x z$ -plane. This is a circular disc $x^{2} + z^{2} \leq 4 .$ So we obtain

\underset{E}{∭} \sqrt{x^{2} + z^{2}} d V = \int_{x = −2}^{x = 2} \int_{y = x^{2}}^{y = 4} \int_{z = − \sqrt{y - x^{2}}}^{z = \sqrt{y - x^{2}}} \sqrt{x^{2} + z^{2}} d z d y d x = \int_{x = −2}^{x = 2} \int_{z = − \sqrt{4 - x^{2}}}^{z = \sqrt{4 - x^{2}}} \int_{y = x^{2} + z^{2}}^{y = 4} \sqrt{x^{2} + z^{2}} d y d z d x .

Here the order of integration changes from being first with respect to $z,$ then $y,$ and then $x$ to being first with respect to $y,$ then to $z,$ and then to $x .$ It will soon be clear how this change can be beneficial for computation. We have

\int_{x = −2}^{x = 2} \int_{z = − \sqrt{4 - x^{2}}}^{z = \sqrt{4 - x^{2}}} \int_{y = x^{2} + z^{2}}^{y = 4} \sqrt{x^{2} + z^{2}} d y d z d x = \int_{x = −2}^{x = 2} \int_{z = − \sqrt{4 - x^{2}}}^{z = \sqrt{4 - x^{2}}} (4 - x^{2} - z^{2}) \sqrt{x^{2} + z^{2}} d z d x .

Now use the polar substitution $x = r cos θ, z = r sin θ,$ and $d z d x = r d r d θ$ in the $x z$ -plane. This is essentially the same thing as when we used polar coordinates in the $x y$ -plane, except we are replacing $y$ by $z .$ Consequently the limits of integration change and we have, by using $r^{2} = x^{2} + z^{2},$

\begin{matrix} \int_{x = −2}^{x = 2} \int_{z = − \sqrt{4 - x^{2}}}^{z = \sqrt{4 - x^{2}}} (4 - x^{2} - z^{2}) \sqrt{x^{2} + z^{2}} d z d x & = \int_{θ = 0}^{θ = 2 π} \int_{r = 0}^{r = 2} (4 - r^{2}) r r d r d θ \\ = \int_{0}^{2 π} [{\frac{4 r^{3}}{3} - \frac{r^{5}}{5} |}_{0}^{2}] d θ = \int_{0}^{2 π} \frac{64}{15} d θ = \frac{128 π}{15} . \end{matrix}

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 1

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 3. OpenStax CNX. Feb 05, 2016 Download for free at http://legacy.cnx.org/content/col11966/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?

Ask

	4 AP 04 Tissue Level of Organization Essay By OpenStax Start Flashcards
	Biology Final By Anonymous User Start Quiz
	9 Arts Society: Theater 9 Exam By Jonathan Long Start Exam
	Pre Employment English Proficiency Exam By Katherina jennife... Start Quiz
	4 Neuroanatomy 04 Spinal Cord Brain Stem By Stephen Voron Start Quiz
	27 AP 27 Reproductive System Essay By OpenStax Start Flashcards
	27 AP 27 Reproductive System MCQ By OpenStax Start Quiz
©flickr: Miguel	Gram Positive Infections and Clostridium By Cath Yu Start Quiz
	22 Muscle and Pancreas Bio Path quiz By Brooke Delaney Start Exam
	Object Oriented Programming Test 1 By Ali Sid Start Test