| << Chapter < Page | Chapter >> Page > |
Double integrals are sometimes much easier to evaluate if we change rectangular coordinates to polar coordinates. However, before we describe how to make this change, we need to establish the concept of a double integral in a polar rectangular region.
When we defined the double integral for a continuous function in rectangular coordinates—say, over a region in the -plane—we divided into subrectangles with sides parallel to the coordinate axes. These sides have either constant -values and/or constant -values. In polar coordinates, the shape we work with is a polar rectangle , whose sides have constant -values and/or constant -values. This means we can describe a polar rectangle as in [link] (a), with
In this section, we are looking to integrate over polar rectangles. Consider a function over a polar rectangle We divide the interval into subintervals of length and divide the interval into subintervals of width This means that the circles and rays for and divide the polar rectangle into smaller polar subrectangles ( [link] (b)).
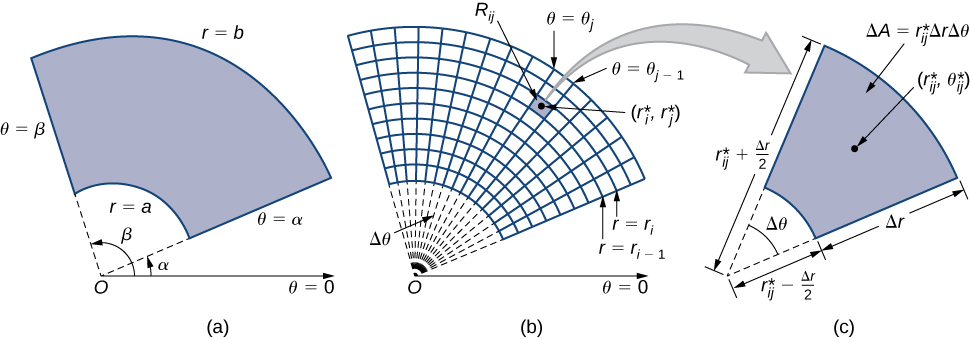
As before, we need to find the area of the polar subrectangle and the “polar” volume of the thin box above Recall that, in a circle of radius the length of an arc subtended by a central angle of radians is Notice that the polar rectangle looks a lot like a trapezoid with parallel sides and and with a width Hence the area of the polar subrectangle is
Simplifying and letting we have Therefore, the polar volume of the thin box above ( [link] ) is
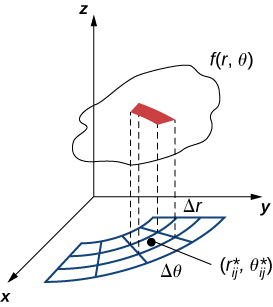
Using the same idea for all the subrectangles and summing the volumes of the rectangular boxes, we obtain a double Riemann sum as
As we have seen before, we obtain a better approximation to the polar volume of the solid above the region when we let and become larger. Hence, we define the polar volume as the limit of the double Riemann sum,
This becomes the expression for the double integral.
The double integral of the function over the polar rectangular region in the -plane is defined as
Again, just as in Double Integrals over Rectangular Regions , the double integral over a polar rectangular region can be expressed as an iterated integral in polar coordinates. Hence,

Notification Switch
Would you like to follow the 'Calculus volume 3' conversation and receive update notifications?