| << Chapter < Page | Chapter >> Page > |





Khan academy video on area and perimeter
Khan academy video on area of a circle
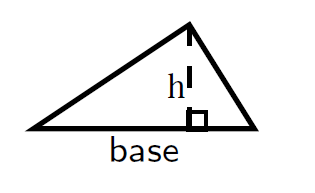
Find the area of the following figure:


In this section we study how to calculate the surface areas and volumes of right prisms and cylinders. A right prism is a polygon that has been stretched out into a tube so that the height of the tube is perpendicular to the base (the definition is motivated by the fact that the angle between base and side form a right angle). A square prism has a base that is a square and a triangular prism has a base that is a triangle.

It is relatively simple to calculate the surface areas and volumes of prisms.
The term surface area refers to the total area of the exposed or outside surfaces of a prism. This is easier to understand if you imagine the prism as a solid object.
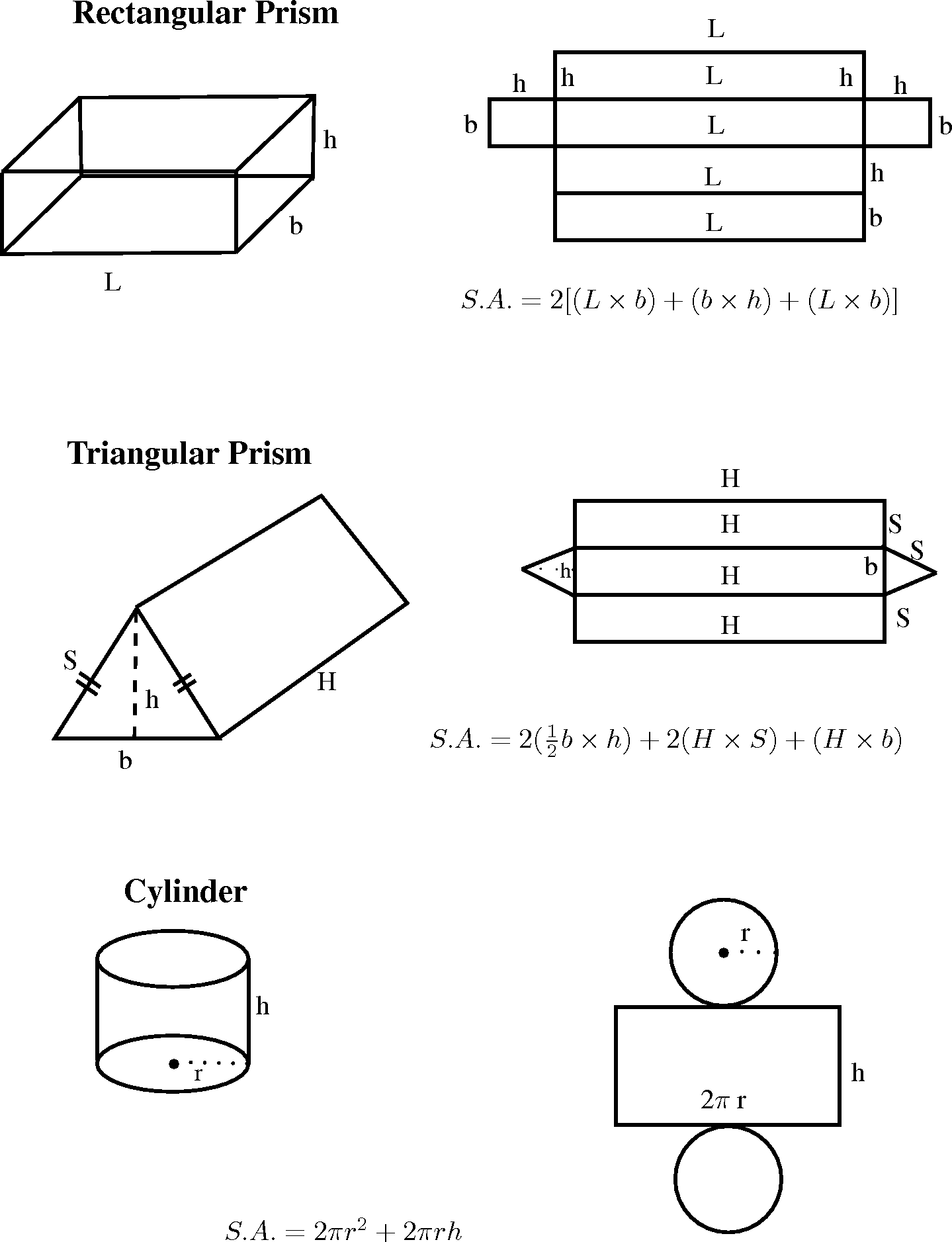
If you examine the prisms in [link] , you will see that each face of a prism is a simple polygon. For example, the triangular prism has two faces that are triangles and three faces that are rectangles. Therefore, in order to calculate the surface area of a prism you simply have to calculate the area of each face and add it up. In the case of a cylinder the top and bottom faces are circles, while the curved surface flattens into a rectangle.
Surface Area of Prisms
Calculate the area of each face and add the areas together to get the surface area. To do this you need to determine the correct shape of each and every face of the prism and then for each one determine the surface area. The sum of the surface areas of all the faces will give you the total surface area of the prism.
In pairs, study the following prisms and the adjacent image showing the various surfaces that make up the prism. Explain to your partner, how each relates to the other.
Find (or take one yourself) a picture of a building that does not have a well defined shape (i.e. is not simply a rectangle). For example a castle with towers, or a house with gable windows or a porch. Assume you have to paint the outside of the building. How much paint would you need? Think about what you have learnt about surface area and the area of polygons. Can you find regular polygons on your picture and use those to find the surface area?

Notification Switch
Would you like to follow the 'Siyavula textbooks: grade 10 maths [caps]' conversation and receive update notifications?