| << Chapter < Page | Chapter >> Page > |
Apparently, the difference between “the same percentage” and “the same amount” is quite significant. For exponential growth, over equal increments, the constant multiplicative rate of change resulted in doubling the output whenever the input increased by one. For linear growth, the constant additive rate of change over equal increments resulted in adding 2 to the output whenever the input was increased by one.
The general form of the exponential function is where is any nonzero number, is a positive real number not equal to 1.
Let’s look at the function from our example. We will create a table ( [link] ) to determine the corresponding outputs over an interval in the domain from to
Let us examine the graph of by plotting the ordered pairs we observe on the table in [link] , and then make a few observations.
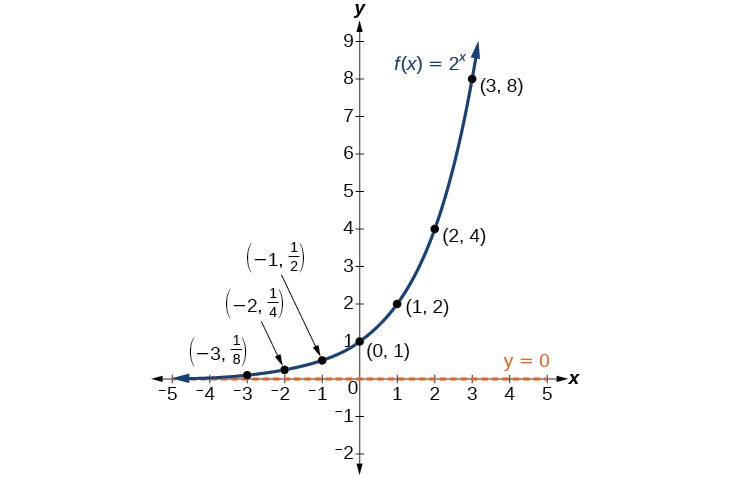
Let’s define the behavior of the graph of the exponential function and highlight some its key characteristics.
For any real number an exponential function is a function with the form
where
Which of the following equations are not exponential functions?
By definition, an exponential function has a constant as a base and an independent variable as an exponent. Thus, does not represent an exponential function because the base is an independent variable. In fact, is a power function.
Recall that the base b of an exponential function is always a positive constant, and Thus, does not represent an exponential function because the base, is less than
Which of the following equations represent exponential functions?
and represent exponential functions.
Recall that the base of an exponential function must be a positive real number other than Why do we limit the base to positive values? To ensure that the outputs will be real numbers. Observe what happens if the base is not positive:
Why do we limit the base to positive values other than Because base results in the constant function. Observe what happens if the base is

Notification Switch
Would you like to follow the 'Precalculus' conversation and receive update notifications?