| << Chapter < Page | Chapter >> Page > |
We have already studied how to find equations of tangent lines to functions and the rate of change of a function at a specific point. In all these cases we had the explicit equation for the function and differentiated these functions explicitly. Suppose instead that we want to determine the equation of a tangent line to an arbitrary curve or the rate of change of an arbitrary curve at a point. In this section, we solve these problems by finding the derivatives of functions that define implicitly in terms of
In most discussions of math, if the dependent variable is a function of the independent variable we express y in terms of If this is the case, we say that is an explicit function of For example, when we write the equation we are defining y explicitly in terms of On the other hand, if the relationship between the function and the variable is expressed by an equation where is not expressed entirely in terms of we say that the equation defines y implicitly in terms of For example, the equation defines the function implicitly.
Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions (they fail the vertical line test). We are using the idea that portions of are functions that satisfy the given equation, but that is not actually a function of
In general, an equation defines a function implicitly if the function satisfies that equation. An equation may define many different functions implicitly. For example, the functions
and which are illustrated in [link] , are just three of the many functions defined implicitly by the equation
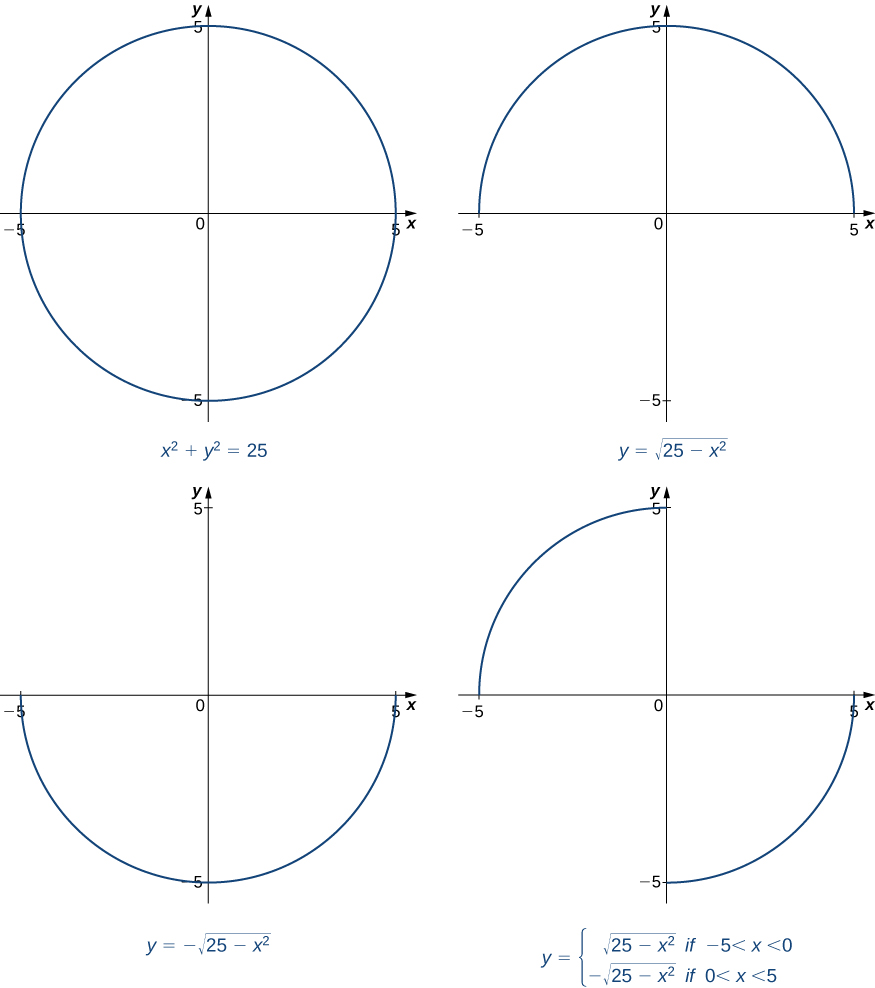
If we want to find the slope of the line tangent to the graph of at the point we could evaluate the derivative of the function at On the other hand, if we want the slope of the tangent line at the point we could use the derivative of However, it is not always easy to solve for a function defined implicitly by an equation. Fortunately, the technique of implicit differentiation allows us to find the derivative of an implicitly defined function without ever solving for the function explicitly. The process of finding using implicit differentiation is described in the following problem-solving strategy.
To perform implicit differentiation on an equation that defines a function implicitly in terms of a variable use the following steps:

Notification Switch
Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?