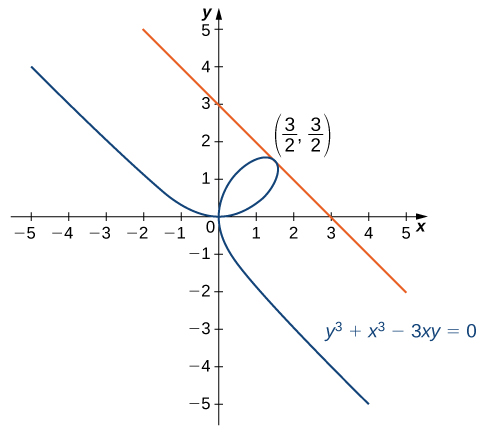3.8 Implicit differentiation (Page 2/4)

Calculus volume 1 Page 2 / 4

Using implicit differentiation

Assuming that $y$ is defined implicitly by the equation $x^{2} + y^{2} = 25,$ find $\frac{d y}{d x} .$

Follow the steps in the problem-solving strategy.

\begin{matrix} \frac{d}{d x} (x^{2} + y^{2}) & = & \frac{d}{d x} (25) & Step 1. Differentiate both sides of the equation. \\ \frac{d}{d x} (x^{2}) + \frac{d}{d x} (y^{2}) & = & 0 & \begin{matrix} Step 1.1. Use the sum rule on the left. \\ On the right \frac{d}{d x} (25) = 0 . \end{matrix} \\ 2 x + 2 y \frac{d y}{d x} & = & 0 & \begin{matrix} Step 1.2. Take the derivatives, so \frac{d}{d x} (x^{2}) = 2 x \\ and \frac{d}{d x} (y^{2}) = 2 y \frac{d y}{d x} . \end{matrix} \\ 2 y \frac{d y}{d x} & = & −2 x & \begin{matrix} Step 2. Keep the terms with \frac{d y}{d x} on the left. \\ Move the remaining terms to the right. \end{matrix} \\ \frac{d y}{d x} & = & - \frac{x}{y} & \begin{matrix} Step 4. Divide both sides of the equation by \\ 2 y . (Step 3 does not apply in this case.) \end{matrix} \end{matrix}

Got questions? Get instant answers now!

Using implicit differentiation and the product rule

Assuming that $y$ is defined implicitly by the equation $x^{3} sin y + y = 4 x + 3,$ find $\frac{d y}{d x} .$

\begin{matrix} \frac{d}{d x} (x^{3} sin y + y) & = & \frac{d}{d x} (4 x + 3) & Step 1: Differentiate both sides of the equation. \\ \frac{d}{d x} (x^{3} sin y) + \frac{d}{d x} (y) & = & 4 & \begin{matrix} Step 1.1: Apply the sum rule on the left. \\ On the right, \frac{d}{d x} (4 x + 3) = 4 . \end{matrix} \\ (\frac{d}{d x} (x^{3}) \cdot sin y + \frac{d}{d x} (sin y) \cdot x^{3}) + \frac{d y}{d x} & = & 4 & \begin{matrix} Step 1.2: Use the product rule to find \\ \frac{d}{d x} (x^{3} sin y) . Observe that \frac{d}{d x} (y) = \frac{d y}{d x} . \end{matrix} \\ 3 x^{2} sin y + (cos y \frac{d y}{d x}) \cdot x^{3} + \frac{d y}{d x} & = & 4 & \begin{matrix} Step 1.3: We know \frac{d}{d x} (x^{3}) = 3 x^{2} . Use the \\ chain rule to obtain \frac{d}{d x} (sin y) = cos y \frac{d y}{d x} . \end{matrix} \\ x^{3} cos y \frac{d y}{d x} + \frac{d y}{d x} & = & 4 - 3 x^{2} sin y & \begin{matrix} Step 2: Keep all terms containing \frac{d y}{d x} on the \\ left. Move all other terms to the right. \end{matrix} \\ \frac{d y}{d x} (x^{3} cos y + 1) & = & 4 - 3 x^{2} sin y & Step 3: Factor out \frac{d y}{d x} on the left. \\ \frac{d y}{d x} & = & \frac{4 - 3 x^{2} sin y}{x^{3} cos y + 1} & \begin{matrix} Step 4: Solve for \frac{d y}{d x} by dividing both sides of \\ the equation by x^{3} cos y + 1 . \end{matrix} \end{matrix}

Got questions? Get instant answers now!

Using implicit differentiation to find a second derivative

Find $\frac{d^{2} y}{d x^{2}}$ if $x^{2} + y^{2} = 25 .$

In [link] , we showed that $\frac{d y}{d x} = - \frac{x}{y} .$ We can take the derivative of both sides of this equation to find $\frac{d^{2} y}{d x^{2}} .$

\begin{matrix} \frac{d^{2} y}{d x^{2}} & = \frac{d}{d y} (- \frac{x}{y}) & Differentiate both sides of \frac{d y}{d x} = - \frac{x}{y} . \\ = - \frac{(1 \cdot y - x \frac{d y}{d x})}{y^{2}} & Use the quotient rule to find \frac{d}{d y} (- \frac{x}{y}) . \\ = \frac{− y + x \frac{d y}{d x}}{y^{2}} & Simplify. \\ = \frac{− y + x (- \frac{x}{y})}{y^{2}} & Substitute \frac{d y}{d x} = - \frac{x}{y} . \\ = \frac{− y^{2} - x^{2}}{y^{3}} & Simplify. \end{matrix}

At this point we have found an expression for $\frac{d^{2} y}{d x^{2}} .$ If we choose, we can simplify the expression further by recalling that $x^{2} + y^{2} = 25$ and making this substitution in the numerator to obtain $\frac{d^{2} y}{d x^{2}} = - \frac{25}{y^{3}} .$

Got questions? Get instant answers now!

Find $\frac{d y}{d x}$ for $y$ defined implicitly by the equation $4 x^{5} + tan y = y^{2} + 5 x .$

$\frac{d y}{d x} = \frac{5 - 20 x^{4}}{{sec}^{2} y - 2 y}$

Got questions? Get instant answers now!

Finding tangent lines implicitly

Now that we have seen the technique of implicit differentiation, we can apply it to the problem of finding equations of tangent lines to curves described by equations.

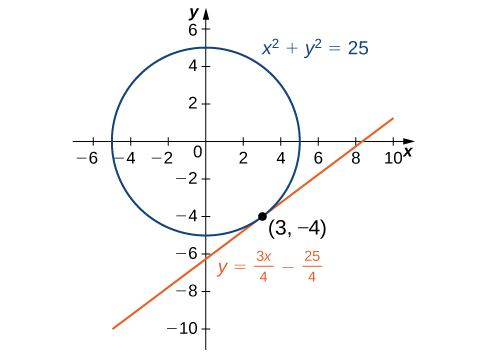
Finding a tangent line to a circle

Find the equation of the line tangent to the curve $x^{2} + y^{2} = 25$ at the point $(3, −4) .$

Although we could find this equation without using implicit differentiation, using that method makes it much easier. In [link] , we found $\frac{d y}{d x} = - \frac{x}{y} .$

The slope of the tangent line is found by substituting $(3, −4)$ into this expression. Consequently, the slope of the tangent line is $\frac{d y}{d x} | \begin{array}{l} _{(3, −4)} \end{array} = - \frac{3}{−4} = \frac{3}{4} .$

Using the point $(3, −4)$ and the slope $\frac{3}{4}$ in the point-slope equation of the line, we obtain the equation $y = \frac{3}{4} x - \frac{25}{4}$ ( [link] ).

The circle with radius 5 and center at the origin is graphed. A tangent line is drawn through the point (3, −4). — The line $y = \frac{3}{4} x - \frac{25}{4}$ is tangent to $x^{2} + y^{2} = 25$ at the point (3, −4).

Got questions? Get instant answers now!

Finding the equation of the tangent line to a curve

Find the equation of the line tangent to the graph of $y^{3} + x^{3} - 3 x y = 0$ at the point $(\frac{3}{2}, \frac{3}{2})$ ( [link] ). This curve is known as the folium (or leaf) of Descartes.

A folium is shown, which is a line that creates a loop that crosses over itself. In this graph, it crosses over itself at (0, 0). Its tangent line from (3/2, 3/2) is shown. — Finding the tangent line to the folium of Descartes at $(\frac{3}{2}, \frac{3}{2}) .$

Begin by finding $\frac{d y}{d x} .$

\begin{matrix} \frac{d}{d x} (y^{3} + x^{3} - 3 x y) & = & \frac{d}{d x} (0) \\ 3 y^{2} \frac{d y}{d x} + 3 x^{2} - (3 y + \frac{d y}{d x} 3 x) & = & 0 \\ \frac{d y}{d x} & = & \frac{3 y - 3 x^{2}}{3 y^{2} - 3 x} . \end{matrix}

Next, substitute $(\frac{3}{2}, \frac{3}{2})$ into $\frac{d y}{d x} = \frac{3 y - 3 x^{2}}{3 y^{2} - 3 x}$ to find the slope of the tangent line:

\frac{d y}{d x} | \begin{array}{l} _{(\frac{3}{2}, \frac{3}{2})} \end{array} = −1 .

Finally, substitute into the point-slope equation of the line to obtain

y = − x + 3 .

Got questions? Get instant answers now!

<< Chapter < Page Page > Chapter >>

Practice Key Terms 1

Read also:

Get Jobilize Job Search Mobile App in your pocket Now!

100% Free Mobile Applications
Receive real-time job alerts and never miss the right job again

Source: OpenStax, Calculus volume 1. OpenStax CNX. Feb 05, 2016 Download for free at http://cnx.org/content/col11964/1.2

Google Play and the Google Play logo are trademarks of Google Inc.

Notification Switch

Would you like to follow the 'Calculus volume 1' conversation and receive update notifications?

Ask

	Financial Markets By Keyaira Braxton Start Exam
	21 Kidney/Liver Biopath By Brooke Delaney Start Exam
	Economy Foundations By Robert Murphy Start Test
©flickr: eLife	Mycobacterial Infections (Mandell 8th Ch 251-254) By Cath Yu Start Quiz
	44 Biology 44 Ecology and the Biosphere MCQ By OpenStax Start Quiz
	Elementary algebra By OpenStax Read Online Course
	Capitalism Market Economy By Robert Murphy Start Test
	6 AP 06 Skeletal System Essay By OpenStax Start Flashcards
	Managerial Psychology Exam By Dan Ariely Start Exam
	7 AP 07 Axial Skeleton MCQ By OpenStax Start Quiz