| << Chapter < Page | Chapter >> Page > |
Given the function express the function as a polynomial in general form and determine the leading term, degree, and end behavior of the function.
The leading term is so it is a degree 3 polynomial. As approaches positive infinity, increases without bound; as approaches negative infinity, decreases without bound.
In addition to the end behavior of polynomial functions, we are also interested in what happens in the “middle” of the function. In particular, we are interested in locations where graph behavior changes. A turning point is a point at which the function values change from increasing to decreasing or decreasing to increasing.
We are also interested in the intercepts. As with all functions, the y- intercept is the point at which the graph intersects the vertical axis. The point corresponds to the coordinate pair in which the input value is zero. Because a polynomial is a function, only one output value corresponds to each input value so there can be only one y- intercept The x- intercepts occur at the input values that correspond to an output value of zero. It is possible to have more than one x- intercept. See [link] .

A turning point of a graph is a point at which the graph changes direction from increasing to decreasing or decreasing to increasing. The y- intercept is the point at which the function has an input value of zero. The x -intercepts are the points at which the output value is zero.
Given a polynomial function, determine the intercepts.
Given the polynomial function written in factored form for your convenience, determine the y - and x -intercepts.
The y- intercept occurs when the input is zero so substitute 0 for
The y- intercept is (0, 8).
The x -intercepts occur when the output is zero.
The x -intercepts are and
We can see these intercepts on the graph of the function shown in [link] .

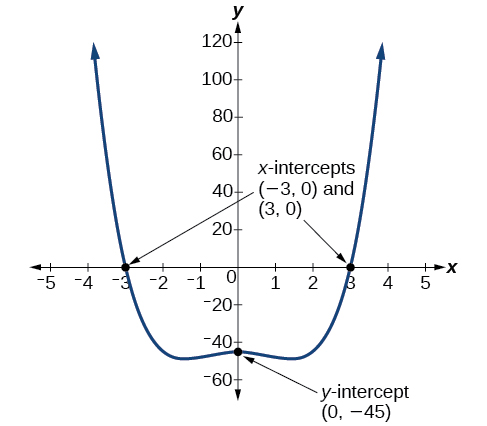
Given the polynomial function determine the y - and x -intercepts.
The y- intercept occurs when the input is zero.
The y- intercept is
The x -intercepts occur when the output is zero. To determine when the output is zero, we will need to factor the polynomial.
The x -intercepts are and
We can see these intercepts on the graph of the function shown in [link] . We can see that the function is even because
Given the polynomial function determine the y - and x -intercepts.
y -intercept x -intercepts and

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?