| << Chapter < Page | Chapter >> Page > |
Describe in words and symbols the end behavior of
As approaches positive or negative infinity, decreases without bound: as because of the negative coefficient.
An oil pipeline bursts in the Gulf of Mexico, causing an oil slick in a roughly circular shape. The slick is currently 24 miles in radius, but that radius is increasing by 8 miles each week. We want to write a formula for the area covered by the oil slick by combining two functions. The radius of the spill depends on the number of weeks that have passed. This relationship is linear.
We can combine this with the formula for the area of a circle.
Composing these functions gives a formula for the area in terms of weeks.
Multiplying gives the formula.
This formula is an example of a polynomial function . A polynomial function consists of either zero or the sum of a finite number of non-zero terms, each of which is a product of a number, called the coefficient of the term, and a variable raised to a non-negative integer power.
Let be a non-negative integer. A polynomial function is a function that can be written in the form
This is called the general form of a polynomial function. Each is a coefficient and can be any real number other than zero. Each expression is a term of a polynomial function .
Which of the following are polynomial functions?
The first two functions are examples of polynomial functions because they can be written in the form where the powers are non-negative integers and the coefficients are real numbers.
Because of the form of a polynomial function, we can see an infinite variety in the number of terms and the power of the variable. Although the order of the terms in the polynomial function is not important for performing operations, we typically arrange the terms in descending order of power, or in general form. The degree of the polynomial is the highest power of the variable that occurs in the polynomial; it is the power of the first variable if the function is in general form. The leading term is the term containing the highest power of the variable, or the term with the highest degree. The leading coefficient is the coefficient of the leading term.
We often rearrange polynomials so that the powers are descending.
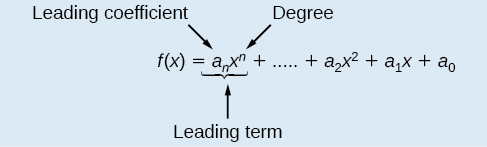
When a polynomial is written in this way, we say that it is in general form.
Given a polynomial function, identify the degree and leading coefficient.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?