| << Chapter < Page | Chapter >> Page > |

To describe the behavior as numbers become larger and larger, we use the idea of infinity. We use the symbol for positive infinity and for negative infinity. When we say that “ approaches infinity,” which can be symbolically written as we are describing a behavior; we are saying that is increasing without bound.
With the positive even-power function, as the input increases or decreases without bound, the output values become very large, positive numbers. Equivalently, we could describe this behavior by saying that as approaches positive or negative infinity, the values increase without bound. In symbolic form, we could write
[link] shows the graphs of and which are all power functions with odd, whole-number powers. Notice that these graphs look similar to the cubic function in the toolkit. Again, as the power increases, the graphs flatten near the origin and become steeper away from the origin.
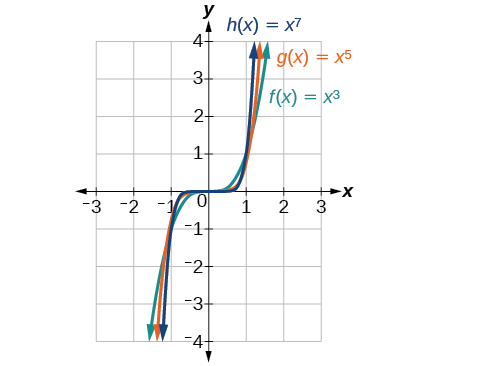
These examples illustrate that functions of the form reveal symmetry of one kind or another. First, in [link] we see that even functions of the form even, are symmetric about the axis. In [link] we see that odd functions of the form odd, are symmetric about the origin.
For these odd power functions, as approaches negative infinity, decreases without bound. As approaches positive infinity, increases without bound. In symbolic form we write
The behavior of the graph of a function as the input values get very small ( ) and get very large ( ) is referred to as the end behavior of the function. We can use words or symbols to describe end behavior.
[link] shows the end behavior of power functions in the form where is a non-negative integer depending on the power and the constant.
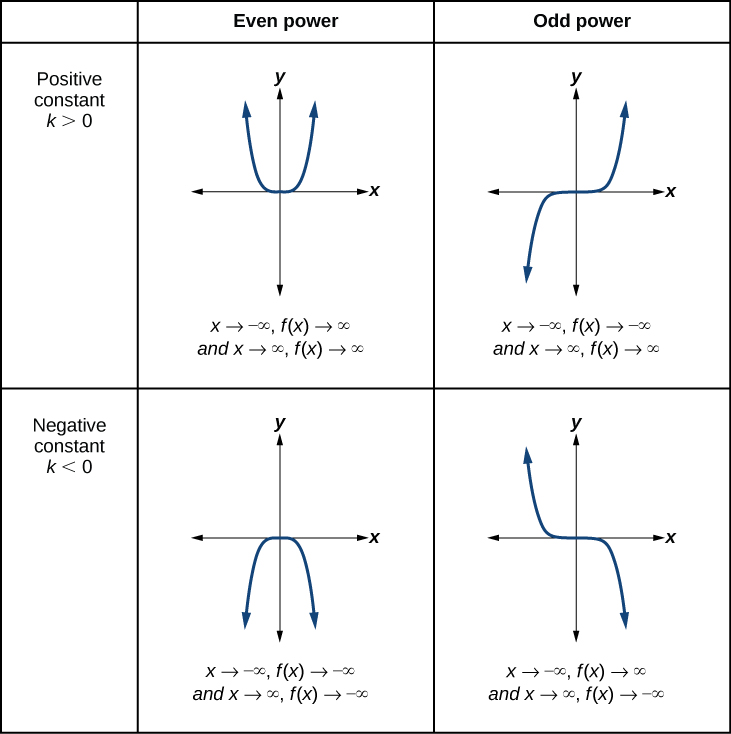
Given a power function where is a non-negative integer, identify the end behavior.
Describe the end behavior of the graph of
The coefficient is 1 (positive) and the exponent of the power function is 8 (an even number). As approaches infinity, the output (value of ) increases without bound. We write as As approaches negative infinity, the output increases without bound. In symbolic form, as We can graphically represent the function as shown in [link] .

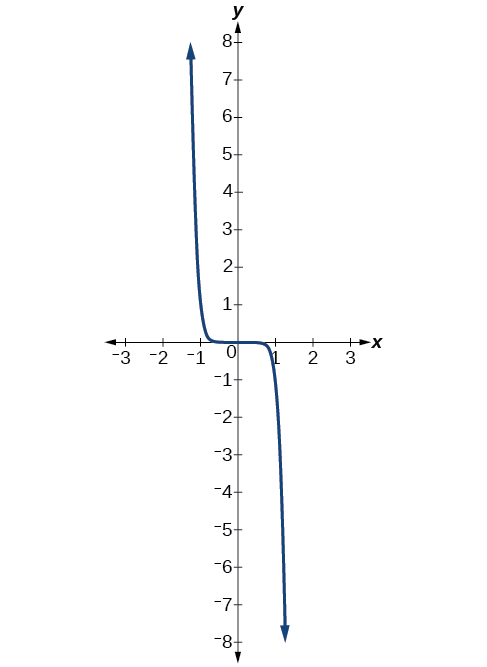
Describe the end behavior of the graph of
The exponent of the power function is 9 (an odd number). Because the coefficient is (negative), the graph is the reflection about the axis of the graph of [link] shows that as approaches infinity, the output decreases without bound. As approaches negative infinity, the output increases without bound. In symbolic form, we would write

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?