| << Chapter < Page | Chapter >> Page > |
Suppose we know that the cost of making a product is dependent on the number of items, produced. This is given by the equation If we want to know the average cost for producing items, we would divide the cost function by the number of items,
The average cost function, which yields the average cost per item for items produced, is
Many other application problems require finding an average value in a similar way, giving us variables in the denominator. Written without a variable in the denominator, this function will contain a negative integer power.
In the last few sections, we have worked with polynomial functions, which are functions with non-negative integers for exponents. In this section, we explore rational functions, which have variables in the denominator.
We have seen the graphs of the basic reciprocal function and the squared reciprocal function from our study of toolkit functions. Examine these graphs, as shown in [link] , and notice some of their features.
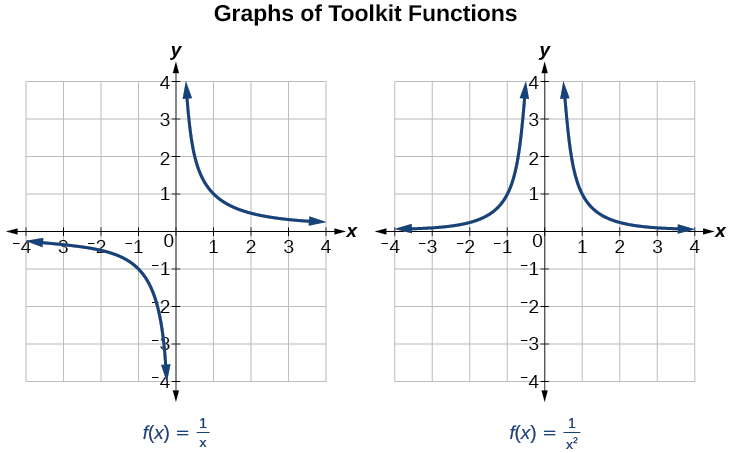
Several things are apparent if we examine the graph of
To summarize, we use arrow notation to show that or is approaching a particular value. See [link] .
| Symbol | Meaning |
|---|---|
| approaches from the left ( but close to ) | |
| approaches from the right ( but close to ) | |
| approaches infinity ( increases without bound) | |
| approaches negative infinity ( decreases without bound) | |
| the output approaches infinity (the output increases without bound) | |
| the output approaches negative infinity (the output decreases without bound) | |
| the output approaches |
Let’s begin by looking at the reciprocal function, We cannot divide by zero, which means the function is undefined at so zero is not in the domain . As the input values approach zero from the left side (becoming very small, negative values), the function values decrease without bound (in other words, they approach negative infinity). We can see this behavior in [link] .
| –0.1 | –0.01 | –0.001 | –0.0001 | |
| –10 | –100 | –1000 | –10,000 |
We write in arrow notation
As the input values approach zero from the right side (becoming very small, positive values), the function values increase without bound (approaching infinity). We can see this behavior in [link] .
| 0.1 | 0.01 | 0.001 | 0.0001 | |
| 10 | 100 | 1000 | 10,000 |
We write in arrow notation
See [link] .
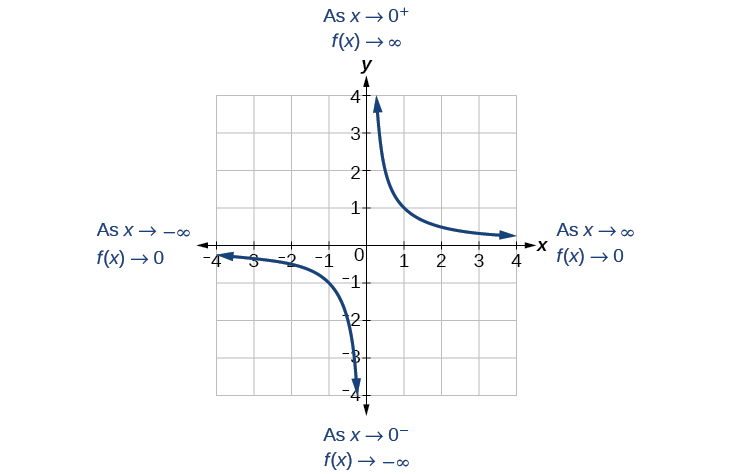
This behavior creates a vertical asymptote , which is a vertical line that the graph approaches but never crosses. In this case, the graph is approaching the vertical line as the input becomes close to zero. See [link] .

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?