| << Chapter < Page | Chapter >> Page > |
The period of a repeating function is the number representing the interval such that for any value of
The period of the cosine, sine, secant, and cosecant functions is
The period of the tangent and cotangent functions is
Find the values of the six trigonometric functions of angle based on [link] .

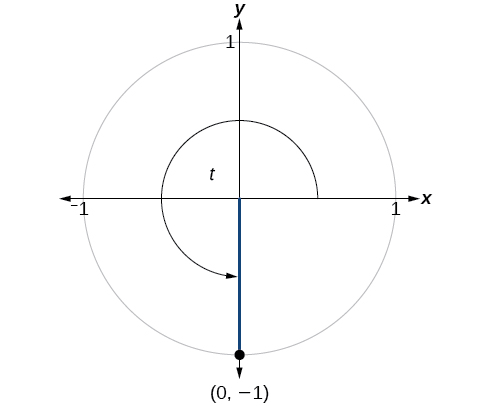
Find the values of the six trigonometric functions of angle based on [link] .
We have learned how to evaluate the six trigonometric functions for the common first-quadrant angles and to use them as reference angles for angles in other quadrants. To evaluate trigonometric functions of other angles, we use a scientific or graphing calculator or computer software. If the calculator has a degree mode and a radian mode, confirm the correct mode is chosen before making a calculation.
Evaluating a tangent function with a scientific calculator as opposed to a graphing calculator or computer algebra system is like evaluating a sine or cosine: Enter the value and press the TAN key. For the reciprocal functions, there may not be any dedicated keys that say CSC, SEC, or COT. In that case, the function must be evaluated as the reciprocal of a sine, cosine, or tangent.
If we need to work with degrees and our calculator or software does not have a degree mode, we can enter the degrees multiplied by the conversion factor to convert the degrees to radians. To find the secant of we could press
Given an angle measure in radians, use a scientific calculator to find the cosecant.
Given an angle measure in radians, use a graphing utility/calculator to find the cosecant.
Evaluate the cosecant of
For a scientific calculator, enter information as follows:
Access these online resources for additional instruction and practice with other trigonometric functions.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?