| << Chapter < Page | Chapter >> Page > |
Because we know the sine and cosine values for these angles, we can use identities to evaluate the other functions.
Simplify
We can simplify this by rewriting both functions in terms of sine and cosine.
By showing that can be simplified to we have, in fact, established a new identity.
We can use these fundamental identities to derive alternate forms of the Pythagorean Identity, One form is obtained by dividing both sides by
The other form is obtained by dividing both sides by
If and is in quadrant IV, as shown in [link] , find the values of the other five trigonometric functions.
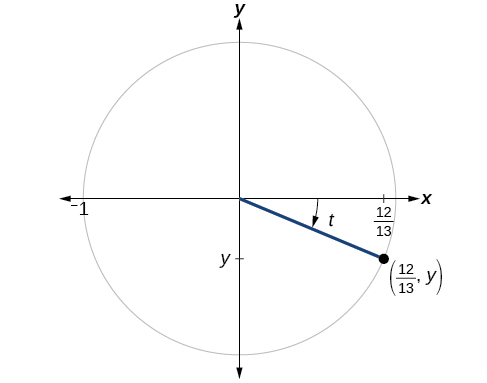
We can find the sine using the Pythagorean Identity, and the remaining functions by relating them to sine and cosine.
The sign of the sine depends on the y -values in the quadrant where the angle is located. Since the angle is in quadrant IV, where the y -values are negative, its sine is negative,
The remaining functions can be calculated using identities relating them to sine and cosine.
As we discussed at the beginning of the chapter, a function that repeats its values in regular intervals is known as a periodic function. The trigonometric functions are periodic. For the four trigonometric functions, sine, cosine, cosecant and secant, a revolution of one circle, or will result in the same outputs for these functions. And for tangent and cotangent, only a half a revolution will result in the same outputs.
Other functions can also be periodic. For example, the lengths of months repeat every four years. If represents the length time, measured in years, and represents the number of days in February, then This pattern repeats over and over through time. In other words, every four years, February is guaranteed to have the same number of days as it did 4 years earlier. The positive number 4 is the smallest positive number that satisfies this condition and is called the period. A period is the shortest interval over which a function completes one full cycle—in this example, the period is 4 and represents the time it takes for us to be certain February has the same number of days.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?