| << Chapter < Page | Chapter >> Page > |
Graph the following equation relative to the system:
First, we find
Because we can draw a reference triangle as in [link] .

Thus, the hypotenuse is
Next, we find and We will use half-angle identities.
Now we find and
and
Now we substitute and into
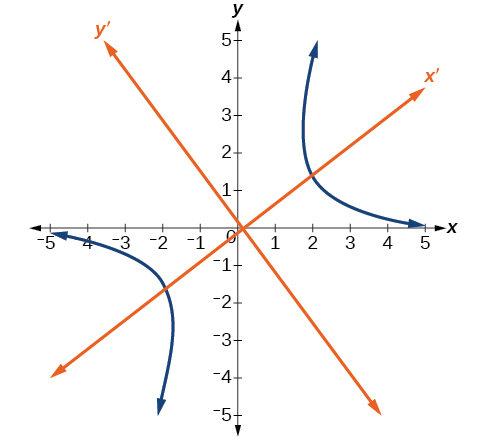
[link] shows the graph of the hyperbola
Now we have come full circle. How do we identify the type of conic described by an equation? What happens when the axes are rotated? Recall, the general form of a conic is
If we apply the rotation formulas to this equation we get the form
It may be shown that The expression does not vary after rotation, so we call the expression invariant . The discriminant, is invariant and remains unchanged after rotation. Because the discriminant remains unchanged, observing the discriminant enables us to identify the conic section.
If the equation is transformed by rotating axes into the equation then
The equation is an ellipse, a parabola, or a hyperbola, or a degenerate case of one of these.
If the discriminant, is
Identify the conic for each of the following without rotating axes.
Now, we find the discriminant.
Therefore, represents an ellipse.
Now, we find the discriminant.
Therefore, represents an ellipse.

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?