| << Chapter < Page | Chapter >> Page > |

Did you know that the Olympic torch is lit several months before the start of the games? The ceremonial method for lighting the flame is the same as in ancient times. The ceremony takes place at the Temple of Hera in Olympia, Greece, and is rooted in Greek mythology, paying tribute to Prometheus, who stole fire from Zeus to give to all humans. One of eleven acting priestesses places the torch at the focus of a parabolic mirror (see [link] ), which focuses light rays from the sun to ignite the flame.
Parabolic mirrors (or reflectors) are able to capture energy and focus it to a single point. The advantages of this property are evidenced by the vast list of parabolic objects we use every day: satellite dishes, suspension bridges, telescopes, microphones, spotlights, and car headlights, to name a few. Parabolic reflectors are also used in alternative energy devices, such as solar cookers and water heaters, because they are inexpensive to manufacture and need little maintenance. In this section we will explore the parabola and its uses, including low-cost, energy-efficient solar designs.
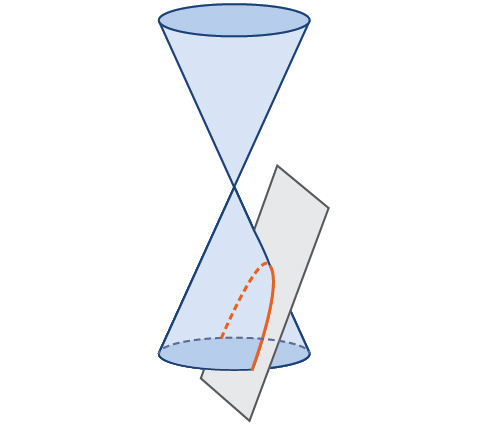
In The Ellipse , we saw that an ellipse is formed when a plane cuts through a right circular cone. If the plane is parallel to the edge of the cone, an unbounded curve is formed. This curve is a parabola . See [link] .
Like the ellipse and hyperbola , the parabola can also be defined by a set of points in the coordinate plane. A parabola is the set of all points in a plane that are the same distance from a fixed line, called the directrix , and a fixed point (the focus ) not on the directrix.
In Quadratic Functions , we learned about a parabola’s vertex and axis of symmetry. Now we extend the discussion to include other key features of the parabola. See [link] . Notice that the axis of symmetry passes through the focus and vertex and is perpendicular to the directrix. The vertex is the midpoint between the directrix and the focus.
The line segment that passes through the focus and is parallel to the directrix is called the latus rectum . The endpoints of the latus rectum lie on the curve. By definition, the distance from the focus to any point on the parabola is equal to the distance from to the directrix.

To work with parabolas in the coordinate plane , we consider two cases: those with a vertex at the origin and those with a vertex at a point other than the origin. We begin with the former.

Let be a point on the parabola with vertex focus and directrix as shown in [link] . The distance from point to point on the directrix is the difference of the y -values: The distance from the focus to the point is also equal to and can be expressed using the distance formula .

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?