| << Chapter < Page | Chapter >> Page > |
between and
between and
For the following exercises, find the zeros and give the multiplicity of each.
0 with multiplicity 2, with multiplicity 5, 4 with multiplicity 2
For the following exercises, graph the polynomial functions. Note and intercepts, multiplicity, and end behavior.
x -intercepts, with multiplicity 2, with multiplicity 1, intercept As
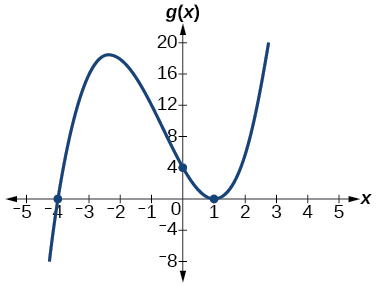
x -intercepts with multiplicity 3, with multiplicity 2, intercept As

For the following exercises, use the graphs to write the formula for a polynomial function of least degree.
For the following exercises, use the graph to identify zeros and multiplicity.
For the following exercises, use the given information about the polynomial graph to write the equation.
Degree 3. Zeros at and y -intercept at
Degree 5. Roots of multiplicity 2 at and , and a root of multiplicity 1 at y -intercept at
Degree 4. Root of multiplicity 2 at and a roots of multiplicity 1 at and y -intercept at
Degree 5. Double zero at and triple zero at Passes through the point
Degree 3. Zeros at and y -intercept at
Degree 5. Roots of multiplicity 2 at and and a root of multiplicity 1 at
y -intercept at
Degree 4. Roots of multiplicity 2 at and roots of multiplicity 1 at and
y -intercept at
Double zero at and triple zero at Passes through the point
For the following exercises, use a calculator to approximate local minima and maxima or the global minimum and maximum.
For the following exercises, use the graphs to write a polynomial function of least degree.
For the following exercises, write the polynomial function that models the given situation.
A rectangle has a length of 10 units and a width of 8 units. Squares of by units are cut out of each corner, and then the sides are folded up to create an open box. Express the volume of the box as a polynomial function in terms of
Consider the same rectangle of the preceding problem. Squares of by units are cut out of each corner. Express the volume of the box as a polynomial in terms of
A square has sides of 12 units. Squares by units are cut out of each corner, and then the sides are folded up to create an open box. Express the volume of the box as a function in terms of
A cylinder has a radius of units and a height of 3 units greater. Express the volume of the cylinder as a polynomial function.
A right circular cone has a radius of and a height 3 units less. Express the volume of the cone as a polynomial function. The volume of a cone is for radius and height

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?