| << Chapter < Page | Chapter >> Page > |
The gravitational force on a planet a distance r from the sun is given by the function The acceleration of a planet subjected to any force is given by the function Form a meaningful composition of these two functions, and explain what it means.
A gravitational force is still a force, so makes sense as the acceleration of a planet at a distance r from the Sun (due to gravity), but does not make sense.
Once we compose a new function from two existing functions, we need to be able to evaluate it for any input in its domain. We will do this with specific numerical inputs for functions expressed as tables, graphs, and formulas and with variables as inputs to functions expressed as formulas. In each case, we evaluate the inner function using the starting input and then use the inner function’s output as the input for the outer function.
When working with functions given as tables, we read input and output values from the table entries and always work from the inside to the outside. We evaluate the inside function first and then use the output of the inside function as the input to the outside function.
To evaluate we start from the inside with the input value 3. We then evaluate the inside expression using the table that defines the function We can then use that result as the input to the function so is replaced by 2 and we get Then, using the table that defines the function we find that
To evaluate we first evaluate the inside expression using the first table: Then, using the table for we can evaluate
[link] shows the composite functions and as tables.
| 3 | 2 | 8 | 3 | 2 |
When we are given individual functions as graphs, the procedure for evaluating composite functions is similar to the process we use for evaluating tables. We read the input and output values, but this time, from the and axes of the graphs.
Given a composite function and graphs of its individual functions, evaluate it using the information provided by the graphs.
To evaluate we start with the inside evaluation. See [link] .
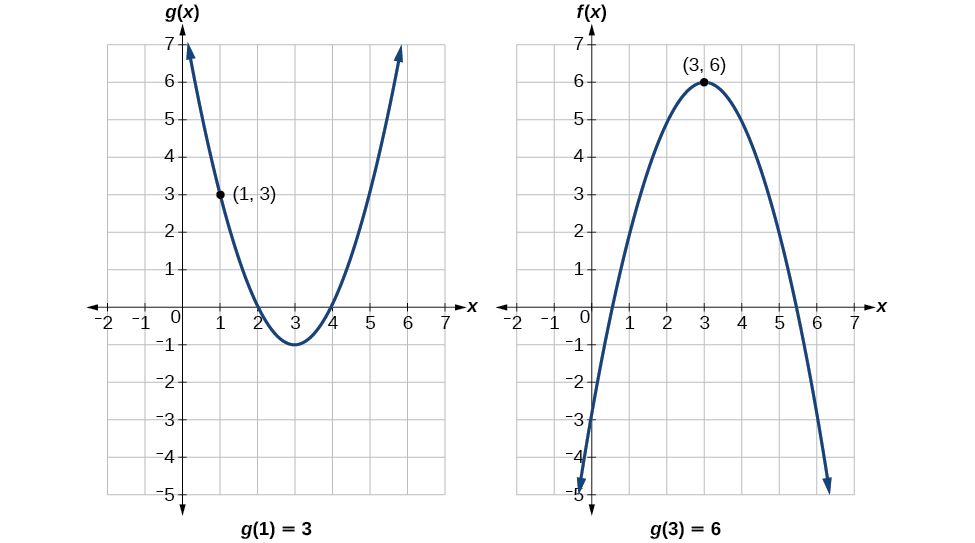
We evaluate using the graph of finding the input of 1 on the axis and finding the output value of the graph at that input. Here, We use this value as the input to the function
We can then evaluate the composite function by looking to the graph of finding the input of 3 on the axis and reading the output value of the graph at this input. Here, so

Notification Switch
Would you like to follow the 'Algebra and trigonometry' conversation and receive update notifications?